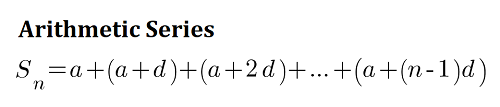Sum of Series Calculator

Our sum of series calculator can calculate the sum of arithmetic series and geometric series. You can also use it to judge whether your series converges or diverges. If you want to learn how to find the sum of a series, you've come to the right place! Here, we shall discuss the arithmetic and geometric series and how to calculate the partial sum of these infinite series.

If you want to switch to a different topic, our independent events calculator will teach you how to deal with the probabilities of three events.

Consider the sequence 2, 4, 6, 8, 10, 12, 14, 16, 18, 20. It is a sequence of the first ten even numbers. Each consecutive term is two greater than the previous term. Such a sequence in which the difference between the consecutive terms is constant is an arithmetic sequence.

Arithmetic series is the sum of an arithmetic sequence. The sum of the first ten even numbers is the arithmetic series:
2 + 4 + 6 + 8 + 10 + 12 + 14 + 16 + 18 + 20 = 110.

While adding individual terms is viable for small-sized sequences, let's formulate an equation to calculate the sum of arithmetic sequences with many terms.

We can find the sum of an arithmetic series if the series has a finite number of terms. The sum of the series formula for an arithmetic series is given by:

where:

• $S_n$ - Sum of the arithmetic series;
• $n$ - The total number of terms in the series;
• $a_1$ - The first term in the series; and
• $d$ - The common difference between any two consecutive terms.

Consider the sequence of the first 100 natural numbers:
1, 2, 3, ..., 99, 100.
Note that this is an arithmetic sequence with a common difference of one.
Hence, we can find the sum of the first 100 natural numbers using the sum of the series formula:

Consider the sequence 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024. It is the first ten powers of 2. Such a sequence where the ratio between any two consecutive terms is constant is a geometric sequence. (Do not confuse this with a factorial).

Geometric series is the sum of a geometric sequence. Before we calculate the sum of a geometric series, we must check whether the series converges or diverges. Whether an infinite geometric series converges or not depends on the common ratio r:

• If |r| > 1, the infinite geometric series diverges. Calculating an infinite series sum is impossible.

• If |r| < 1, the infinite geometric series converges. Calculating an infinite series sum is possible.

• If |r| = 1, the absolute value of each term is constant. Calculating an infinite geometric series sum is impossible.

One of the examples of geometric series in physics is half life of radioactive decay which has r = 0.5. Check our another tool to learn more about calculating half life.

When the common ratio |r| < 1, we can calculate the infinite geometric series sum with the formula:

where:

• $S$ - The sum of infinite geometric series;
• $a$ - The first term in the infinite series; and
• $r$ - The common ratio between any two consecutive terms.

Consider the infinite geometric series: 1, 0.1, 0.01, 0.001, .... The common ratio is 0.1 or 1/10. Hence, this series is convergent, and its sum is:

The line over the decimal digit indicates a non-terminating repeating decimal.

The 2^k geometric series (2 + 4 + 8 + 16 + ...) diverges since r = 2, so calculating an infinite series sum is impossible. However, we can calculate a partial sum for a finite number of terms:

where:

• $S_n$ - The partial sum of first $n$ terms of a geometric series;
• $a$ - The first term; and
• $r$ - The common ratio.

The sum of the first 10 terms of the 2^k geometric series would be:

Now you know how to find the sum of any series.

This sum of a series calculator makes it easy to find the sum of an arithmetic series or a geometric series.

To calculate the sum of an arithmetic sequence:

• Select arithmetic in the field series type.
• Enter the proper values for the first term (a), the common difference (d), and the number of terms (n).
• This sum of a series calculator will give you the arithmetic series sum automatically.

To calculate the sum of a geometric series:

• Select geometric in the field series type.
• Enter the correct values for the first term (a) and the common ratio (r).
  • If the series is convergent, this calculator will automatically calculate the sum of the infinite geometric series.
  • If the series is divergent, you need to enter a value for the number of terms (n) in order to calculate a partial sum of the geometric series.