Rocket Equation Calculator

From probes flying over Pluto to satellites for television, calculating the rocket equation is fundamental in astrodynamics. With our tool, you will learn:

• What is Tsiolkovsky rocket equation;
• How to derive the rocket equation;
• How to calculate the rocket equation for an ideal rocket;
• How to use the formula for the velocity of a rocket.

And much more. Buckle up, 3, 2, 1... take off!

For millennia humans looked at the sky, wondering, but only at the end of the XIX century was science finally at our side.

Scientists developed the foundations of rocketry, both experimental and theoretical. Among them was a Russian scientist, Konstantin Tsiolkovsky. In May 1987, he finalized the equation that now brings his name, the Tsiolkovsky rocket equation. In his work "" Exploration of Outer Space using Rocket Devices", he envisioned a future where rockets propelled humanity among the planets.

We are not there yet, but his mathematics was sound, allowing our species to walk a first of hesitant steps in space.

But what is the Tsiolkovsky rocket equation? And what do we calculate with the rocket equation?

The Tsiolkovsky equation for a rocket (ideal, as we don't consider many factors in it), relates the initial and final mass of a rocket to the variation in velocity. This simple relationship is crucial in the planning of every kind of spaceflight: let's see the formula of the rocket equation:

Where:

• $\Delta v$ — The variation in velocity (the delta v);
• $v_{\text{e}}$ — The exchaust velocity;
• $m_{\text{i}}$ — The inital mass; and
• $m_{\text{f}}$ — The final mass, after some of the fuel burned.

The derivation of the Tsiolkovsky rocket equation requires starting with the relationship between force and acceleration: we discussed it in our Newton's second law calculator. We set the rate of change in linear momentum to the external forces acting on the body — which are zero since we are dealing with the ideal rocket equation:

The initial and final momentums are:

Here we see the initial and final mass multiplied by the velocity, which in the final moment has an increase of $\Delta v$. In the second expression, we see the contribution of the exhaust, too (relative to the rocket).

Now compute the difference and calculate the limit. We change the sign of the mass variation to a decrease (we are considering a reduction in mass): $\Delta m\rightarrow -\text{d}m$, and we plug the result in the first equality (force-variation in momentum).

First, the difference:

Then:

Now we rearrange the terms and integrate on the proper boundaries:

You derived the rocket equation for the ideal case. It's not that easy when other factors come into play: in particular, a rocket is affected by drag (when in an atmosphere) and by gravity (when it's too close to a massive body). The effect of those forces is complex to mode, but you can learn more about them at ours drag equation calculator and gravitational force calculator.

Tsiolkovsky rocket equation tells us that, for a given engine and a given amount of fuel, we can achieve a specific change in velocity. The knowledge about this change is fundamental when planning a maneuver in space. We can also use the equation in "reverse": we can picture our Solar System with a map of the necessary delta-v for any desired maneuver, like the one below:

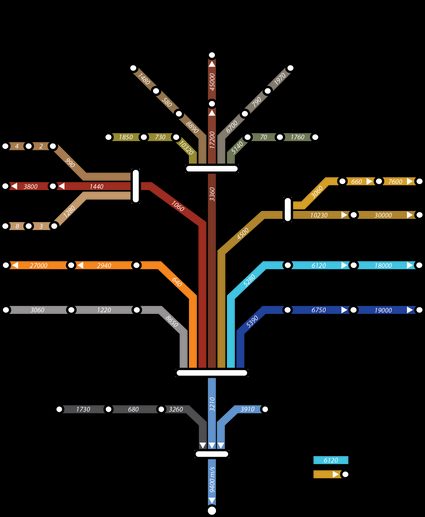
Sum the numbers on the desired branches, choose the dry mass (without fuel) of your craft, the exhaust speed of your engine, and by using the ideal rocket equation, you can find the amount of energy required for the travel. For less complexity but more speculation, you can plan your... star trek with our space travel calculator!

We can calculate the rocket equation in a practical case. Take the delta-v budget map above, and plan a trip from Earth's orbit to, say, Callisto, one of the many moons of Jupiter. There's no need for a formula for the rocket velocity difference, simply sum the values you find in the map:

• From LEO to Earth intercept: $3,120\ \text{m}/\text{s}$;
• FromEarth intercept to Jupiter intercept: $3,360\ \text{m}/\text{s}$ (why so low? There's not much out there to change your trajectory, simply coasting is fine!);
• From Jupiter to Callisto intercept: $5,140\ \text{m}/\text{s}$;
• From Callisto intercept to low orbit: $70\ \text{m}/\text{s}$; and
• From low orbit to landing on Callisto: $1,760\ \text{m}/\text{s}$;

For a total delta v $\Delta v = 13,540\ \text{m}/\text{s}$. Now choose your ride. We will use the same engine we used in the rocket thrust calculator, the RS-68A. We know its exhaust has speed: $v_{\text{e}} = 5,130\ \text{m}/\text{s}$. With a final mass of our spaceship $m_{\text{f}}= 25,000\ \text{kg}$, use our Tsiolkovsky rocket equation calculator to find the amount of fuel needed for the trip:

That's a lot of fuel! There are many ways to change this inconvenient situation: different engines (ionic, nuclear), different propellants, or staging. Or, even better, setting up a colony on the Moon!