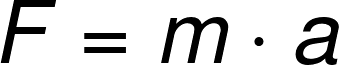Force Calculator

Welcome to our force calculator, where you can calculate the force acting on a body using Newton's second law. We shall address some fundamentals regarding force calculations, so read through this article if you have any of the following nagging questions:

• What is force?
• What is the formula for force?
• What is Newton's second law of motion?
• Is force a scalar or a vector quantity?
• How do you calculate net force?

This force calculator is a simple tool to determine how much force is acting on a system.

• Enter the mass and acceleration of the body, and the calculator will do the rest.
• Use the different units in the tool to avoid unit conversion hassle.

You can also use this calculator to find the acceleration or the mass of the body by providing the remaining two variables!

A force is any action on a body (with mass) that can change its motion. We perceive this change in motion through a change in the object's velocity (or momentum). Newton's second law states that "the change in the object's momentum is directly proportional to the force applied".
For a constant mass system, the formula for force is given by:

Where:

• $\vec{F}$ is the force acting on a body of mass $m$;
• $\vec{p}$ is the momentum of the body;
• $\vec{v}$ is the velocity of the body; and
• $\vec{a}$ is the acceleration of the body.

As the arrows indicate, force is a vector quantity, acting in the same direction as the acceleration. Use our acceleration calculator to find the acceleration in your case.

The SI unit of force is Newton $(\text{N})$, while the imperial system uses units such as pound-force $(\text{lbf})$ and dynes $(\text{dyn})$.

Let us understand this concept of force through some examples:

1. You need to stop a mass of $200 \text{ kg}$ moving at $25 \text{ m/s}$. Use the force equation to find how much force you need to apply to stop it in $5 \text{ s}$.

Let us list out everything given to us first:
1. Mass, $m = 200 \text{ kg}$.
2. Initial velocity, $u = 25 \text{ m/s}$.
3. Desired final velocity, $v = 0 \text{ m/s}$.
4. Time period in which the velocity changes, $\Delta t = 5 \text{ s}$.

We will need acceleration to calculate force:

The negative symbol indicates the direction of acceleration; In this case, the acceleration is opposite to the direction of velocity.

Using this information, we can determine the force required:

Note that this force with the negative sign acts in the same direction as the acceleration.

If you need to find the velocity from distance and time, use our velocity calculator.

Now let's learn how to find acceleration with mass and force using the force formula.

2. A shopping cart weighing $70\text{ lb}$ is pushed with a force of $35 \text{ N}$. Calculate the cart's acceleration.

Again, let's list out the given data:
1. Mass, $m = 70 \text{ lb}$.
2. Force, $F = 35 \text{ N}$.

Now how do we find acceleration with this mass and force information? Let's rearrange the force equation to get:

Using this equation, we get:

You can avoid all these unit conversions using our calculator instead! Now you know how to find acceleration with mass and force.

When multiple forces act on a body, the net force shall determine the body's motion. Since force is a vector quantity, we determine the net force acting on a body using the vector addition:

Where:

• $R$ is the resultant force or net force;
• $F_i$ are individual forces acting on the body.

Head to our net force calculator to calculate the net force acting on a body.