Normal Force Calculator

This normal force calculator can help you determine the normal force acting on a body placed on a surface, whether the surface is flat or inclined. The following article explores the basics of normal force and Newton's third law of motion. Specifically, let's look at:

• What is the normal force?
• How to calculate the normal force
• How to find the normal force when an external force is acting on the body

Before we dive in, head to our Newton's second law calculator if you need a refresher.

A body placed on a surface exerts a force on the surface due to its weight. By Newton's third law, the surface exerts an equal and opposite force on the body, resulting in equilibrium. This force acting on the body, perpendicular to the surface, is known as the normal force.

Consider the object lying on a horizontal surface, as shown in Figure 1.

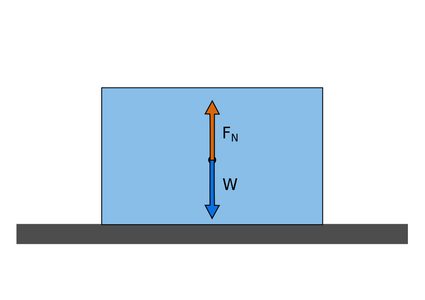
At equilibrium, the force balance will give rise to the normal force equation:

Where:

• $F_N$ - Normal force;
• $W$ - Weight of the body;
• $m$ - Mass of the body; and
• $g$ - Acceleration due to gravity, approximately $9.81 \text{ m/s}^2$.

Now let's turn to inclined surfaces. How do we find the normal force on an incline?

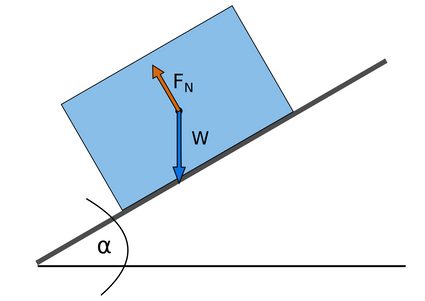
We must resolve the weight $W$ into components perpendicular and parallel to the inclined surface. The component parallel to the inclined surface must be in balance with the frictional force (otherwise, the object will slide down). The component perpendicular to the surface is of interest while calculating normal force:

Where $\alpha$ is the angle of inclination of the surface. This normal force equation is how we find the normal force on an incline.

If an external force is acting on an object lying on a horizontal surface, the normal force calculation will differ. Consider the case where the force is acting downward:

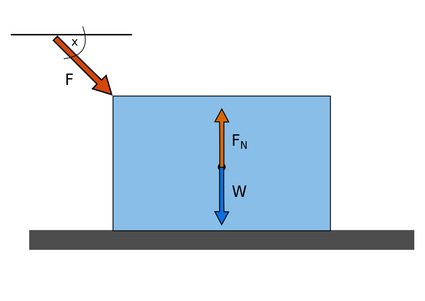
The normal force formula must take the external force component acting perpendicular to the surface:

Where:

• $F$ - External force; and
• $x$ - The angle the line of action of the external force makes with the horizontal.

We added the perpendicular component of the external force to the normal force formula since the external force is acting downward.

Now consider the case where the external force acts upwards:

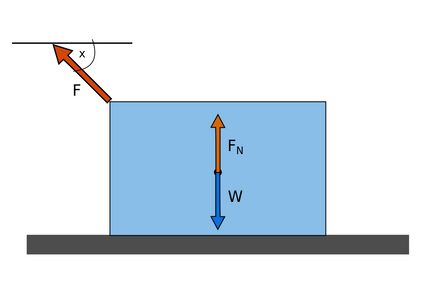
Here, we must subtract the vertical component of the external force to obtain the normal force formula:

If you need help with the trigonometric functions, our trigonometric functions calculator will help you.

We strive to make effective and user-friendly tools. This normal force calculator is no exception:

• Choose the type of surface, between horizontal and inclined.

  • For inclined surfaces, enter the mass and inclination angle values to compute the normal force.

  • For horizontal surfaces, if there is no external force acting on the object, provide the object's mass to calculate the normal force.

  • For horizontal surfaces with an external force, provide the object's mass, the external force, and its *angle, and the normal force will appear automatically. Make sure you select whether the force is acting upward or downward.