Capacitors in Series Calculator

Welcome to our "capacitors in series calculator," where you'll be able to evaluate the equivalent capacitance of up to 10 individual capacitors.

Read on to know the formulas for capacitors in series, the relationship between capacitors in series and voltage, and some interesting aspects related to capacitors in series and parallel.

Capacitors are electronic components that store electric charge (or electrical energy). When combined in series, the charge ($Q$) in each capacitor is the same, while the total voltage ($V$) equals the sum of voltages over each one separately ($V_1$, $V_2$, ..., $V_n$).

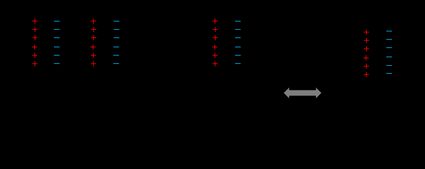
Then, the expression for the total voltage over the whole circuit is:

while the formula for the voltage over each capacitor is:

As mentioned before, for capacitors in series, the voltage of the whole circuit equals the sum of voltages over each one separately:

If we divide each side of the previous equation by $Q$, we get:

In plain English, total capacitance equals the sum of the inverse of every capacitance. That one is the formula with which we calculate capacitors in series in this calculator.

As you may figure out in the last section, the arrangement of capacitors in series results in a lower total capacitance than combining capacitors in parallel.

We can also use capacitors in combination with other systems:

• RC circuits consist of a group of resistors and capacitors, either in series or parallel.
• Voltage dividers: some of these elements consist of a group of capacitors in series.
• LC circuits: these elements consist of an inductor and a capacitor in series or parallel.
• 555 timer IC: in its astable mode, this circuit uses two capacitors in series to define its characteristic operation times.

There are also some similarities with resistors. The formula for capacitors in series is analog to the equation for parallel resistors. In contrast, for capacitors in parallel, the equation is analog to the equation for resistors in series.