Low Pass Filter Calculator

If you need to keep the high frequencies out of your signal, you can use low-pass filters: calculate the cutoff frequency of the most common filtering circuits.

Read our short article; you will learn:

• What are low-pass filters;
• How to calculate an RC filter's cutoff frequency;
• The RL low-pass filter calculations;
• Active filters: the equations for low-pass filters with op-amp.

A low-pass filter is a versatile, multiply-shaped device with many applications. We can sum them up as two faces of the same coin: you take the one you prefer.

• A low-pass filter cuts the higher frequencies in a signal; or
• A low-pass filter preserves the low frequencies of a modulation.

There is no single description of such devices: in our low-pass filter calculator, we will deal with four of the most common ones:

• The RC filter;
• The LC filter;
• The inverting op-amp filter; and
• The non-inverting op-amp filter.

Even though their design varies greatly, we can easily calculate the cutoff frequency in low-pass filters without dwelling too much on physics and math.

Low-pass filters are much needed in many fields dealing with signals. For example, when you design a loudspeaker they are fundamental to split a signal into frequency bands: learn more at our crossover calculator.

You're likely to have encountered an RC filter before: they are the most common and easily understandable low-pass filters out there. We made an entire tool dedicated to them: the RC circuit calculator!

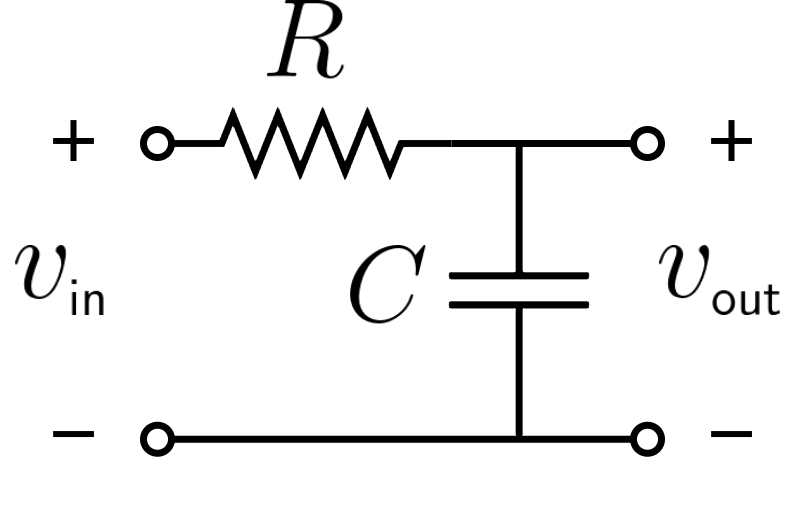
RC stands for resistor and capacitor: our filter only needs these two passive components to operate. The resistance is in series with both the load and the capacitor, and we pick up the signal from the two extremities of the capacitor. Here's a diagram:

The impedance (a quantity almost analog to the resistance) of the capacitor strongly depends on the frequency of the signal, dropping dramatically for high frequencies. In this spectrum region, the capacitor acts as a closed circuit. While the high frequencies pass through the component, the high impedance at low frequencies forces the latter on the parallel, where we pick them up.

We calculate the RC filter cutoff frequency passing through the characteristic time of the RC circuit:

By straightforwardly inverting the equation and adding a constant term:

The next low-pass filter in our calculator is the RL filter. Here we substitute the capacitor with an inductor. The behavior of this filter is not much different from the RC filter; we calculate the RL low-pass filter cutoff frequency with the formula:

We show the circuit for an RL filter in the picture below. As you can see, the position of the elements changed: the inductor behaves in the opposite way of a capacitor, increasing the impedance with frequency.

The inductor blocks the high frequencies while lower frequencies pass undisturbed.

The ultimate low-pass filter is the RLC filter. In this circuit, all three elements appear. Its description, however, is out of the scope of our low-pass filter calculator: we talked about it in detail on our RLC circuit calculator

Active low-pass filters include components with their power source. Adding an external source allows us to amplify the signal in output from the circuit.

Inverting op-amp low-pass filter: formula and gain explanation

In this first active low-pass filter, you can see that the operational amplifier takes the output signal and feeds it back through the feedback resistor $R_{\text{f}}$.

The feedback resistor, together with the capacitor in parallel, determines the cutoff frequency of the low-pass filter: we calculate it with the formula already seen in the RC low-pass filter calculator.

The amplification factor (gain) of the operational amplifier depends on the value of the resistors converging on its input:

We use the value of the gain to calculate the output signal with the formula:

Notice the minus sign? The operational amplifier flips the signal $180\degree$ out of phase. This may not be a big deal, as many devices are unaffected by polarity. However, for specific applications, you may need the...

Non-inverting op-amp low-pass filter

You can see the circuit of an active low-pass filter that doesn't flip the output signal in the picture below.

The formula for the cutoff frequency doesn't change much:

However, since we feed the output on the other input of the operational amplifier, the formula for the gain changes:

The value of $G$ is necessarily greater than 1, thus preserving the polarity of the signal. Mind that this condition also means that you can't reduce the amplitude of your signal when using a non-inverting op-amp filter.