RMS Voltage Calculator

With this RMS voltage calculator, you can determine the RMS voltage value for different waveforms. The RMS voltage gives us a single representative number for an AC circuit rather than a constantly changing value, allowing us to simplify the electrical power calculation of the circuit.

In the accompanying text of this calculator, we'll be discussing:

More about what the RMS voltage is;
How to calculate the RMS voltage; and
The RMS voltage formula for different waveforms.

So sit back, relax, and enjoy learning all about RMS voltage! ⚡

What is the RMS voltage?

Most households work with AC voltage, a type of voltage that continuously alternates between positive and negative values, in contrast to DC voltage, which is constant and doesn't alternate.

When we want to calculate the electrical power $P$ of a DC circuit, we can achieve this by simply multiplying the voltage $V$ and the current $I$ values as:

\small P = V\cdot I

💡 You can check the electrical power calculator and the watt calculator to continue reading about this topic!

But if we'd like to do this same calculation for an AC circuit, how do we do this? Which voltage and current values should we use? A solution to this is to use a single voltage and current values that are representative of the AC circuit. These are the RMS voltage $V_\text{RMS}$ and the RMS current $I_\text{RMS}$ . These two can be understood as representative of the AC signal. We can think of this as the DC equivalent of an AC circuit.

You might wonder why we use the RMS values rather than the average ones. Even though the average could also be a single value representing the AC circuit, the problem arises for some waveforms, such as the sine, whose averages result in zero, so we can't compute the power. To avoid this, we can use the RMS current and voltage.

If you're familiar with RMS (root mean square) definition, you might remember that we can calculate the RMS of a $n$ set of numbers as the square root of the mean square of the values:

\small RMS = \sqrt{\cfrac{1}{n}\left( x_1^2+x_2^2+...+x_n^2\right)}

We use the integral version to calculate the RMS value of a continuous function. Then to find the RMS voltage of a waveform, we use the following RMS voltage formula:

\small V_\text{RMS} = \sqrt{\cfrac{1}{T}\int_0^T{v(t)^2 \, dt}}

where:

$V_\text{RMS}$ – Root mean square voltage, in volts;
$T$ – Period of the signal;
$v(t)$ – Continuous-time waveform.

Finally, to find the electrical power of an AC circuit, we multiply the RMS voltage and current, resulting in the average power of the AC circuit. Check out the AC wattage calculator to keep learning about electrical power in an alternating current circuit.

💡 With the RMS values, you can use Ohm's law. Visit the Ohm's law calculator if you'd like a refresher on how to find the resistance of a circuit using this law.

How to calculate the RMS voltage – RMS voltage formulas

We can use different types of waveforms to describe a signal. Some of the most common waveforms include sinusoidal, square, triangular, and sawtooth. We can apply the general RMS voltage formula in each case to find the RMS voltage $V_\text{RMS}$ . Let's see how to find the RMS voltage for a sine wave $v(t) = V_\text{p}\sin(t)$ :

\small \begin{split} V_\text{RMS} &= \sqrt{\cfrac{1}{T}\int_0^T{\left(V_\text{p}\sin(t)\right)^2 \, dt}} \\ &= \sqrt{\cfrac{1}{\pi} \ V_\text{p}^2\int_0^\pi {\sin(t)^2 \, dt}} \\ &= \sqrt{\left. \cfrac{1}{\pi} \ V_\text{p}^2 \left( \cfrac{t}{2} -\cfrac{\sin(2t)}{4}\right) \right|_{0}^{\pi}} \\ &= \sqrt{\cfrac{ \ V_\text{p}^2}{\pi} \cdot \cfrac{\pi}{2}} \\ &= \sqrt{\cfrac{1}{2}} \ V_\text{p} = \cfrac{\sqrt2}{2} \ V_\text{p} \\[1.1em] &\approx 0.7071 \ V_\text{p} \end{split}

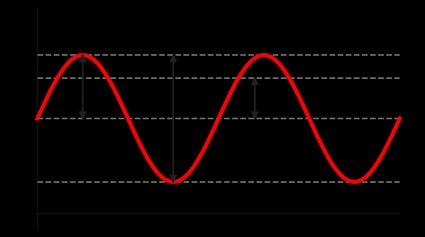
AC sine wave with the peak, peak-to-peak and average voltages.

Note here we integrated from zero to $\pi$ , meaning we determined the RMS voltage from the peak voltage value $V_\text{p}$ . We may alternatively have calculated the RMS voltage from the peak-to-peak $V_{\text{pp}}$ or with the average voltage $V_{\text{avg}}$ .

For the most commonly used waveforms, we don't have to integrate every time we need to find the RMS voltage; instead, we use its corresponding already determined formula. These are simple expressions, which we've compiled in the table below. Here you'll find the RMS of a square wave, triangle wave, among others:

Waveform	RMS voltage
Sine wave	$V_\text{p}/\sqrt{2}$
	$V_\text{pp}/(2\sqrt{2})$
	$\pi V_\text{avg}/(2\sqrt{2})$
Square wave	$V_\text{p}$
	$V_\text{pp}/2$
	$V_\text{avg}$
Triangle wave	$V_\text{p}/\sqrt{3}$
	$V_\text{pp}/(2\sqrt{3})$
	$\pi V_\text{avg}/(2\sqrt{3})$
Sawtooth wave	$V_\text{p}/\sqrt{3}$
	$V_\text{pp}/(2\sqrt{3})$
	$\pi V_\text{avg}/(2\sqrt{3})$
Half-wave rectified sine wave	$V_\text{p}/2$
	$V_\text{pp}/4$
	$\pi V_\text{avg}/2$
Full-wave rectified sine wave	$V_\text{p}/\sqrt{2}$
	$V_\text{pp}/(2\sqrt{2})$
	$\pi V_\text{avg}/(2\sqrt{2})$

Do you need to include the offset voltage $V_0$ in the RMS voltage calculation? To do this, all we have to do is add the square of the offset voltage to the mean of the squares of the signal's amplitude. For example, in the case of a sine wave:

\small V_\text{RMS}=\sqrt{V_0^2 +\left(\cfrac{V_p}{\sqrt2}\right)^2}

🙋 If you like to keep learning more about electric circuits, then you should take a look at the RC circuit calculator or the RLC circuit calculator!

Using the RMS voltage calculator

With this RMS voltage calculator, you can find the RMS value for various waveform shapes. To find the RMS:

Select the Waveform shape. You can choose between sinusoidal, square, triangular, and sawtooth waves and half- or full-rectified sine waves.
Proceed to select the Characteristic voltage of the waveform. You can pick between peak voltage $(V_\text{p})$ , peak-to-peak voltage $(V_\text{pp})$ , or average voltage $(V_\text{avg})$ .
Enter the Voltage value for the selected characteristic voltage.
Input the Wave offset $(V_0)$ .
That's it! ⚡ The calculator will now display the RMS voltage for your inputs.

What is the RMS voltage?

How to calculate the RMS voltage – RMS voltage formulas

Using the RMS voltage calculator

Capacitance

Schwarzschild radius

Wire gauge