Open Channel Flow Calculator

Welcome to our open channel flow calculator! With this tool, you'll easily determine the cross-sectional area, velocity, and volumetric flow rate for the dimensions of the open channel you're designing. The calculations are done employing Manning's equation for flow in open channels.

If you're curious about what's open channel flow or which is the most efficient cross-section for open channels, is it rectangular? or maybe trapezoidal? Then we recommend reading the text below to learn about this.

Open channel flow refers to a type of flow that has a free surface that's in contact with the atmosphere. In contrast to flow in enclosed conduits such as pipes, an open channel flow travels through an open conduit, as in rivers, estuaries, ditches, and sewers. The fluid, generally water, is exposed to atmospheric pressure, making the pressure at the surface remain constant. The pressure difference in these flows is primarily a consequence of gravity. As a result, the force balance is given by gravity and friction.

Open channels flow rate is affected by:

• The material of the walls of the channel;
• The cross-sectional geometry; and
• The slope of the channel.

The roughness of the channel surface walls is directly related to the material. The flow is slowed by the roughness of the channel.

The effect of cross-sectional geometry on flow is related to the amount of flow that can take place. The greater the cross-sectional area, the greater the amount of fluid that can flow. However, the greater the contact surface between the channel's walls and the fluid, the greater the friction that will slow the flow.

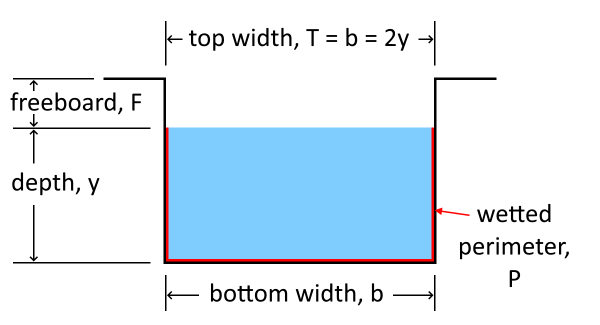
To take this last into account, the wetted perimeter P parameter is used. This one describes the cross-sectional length of the channel that's in contact with the fluid. The larger the wetted perimeter, the more water is in contact with the channel, slowing down the flow.

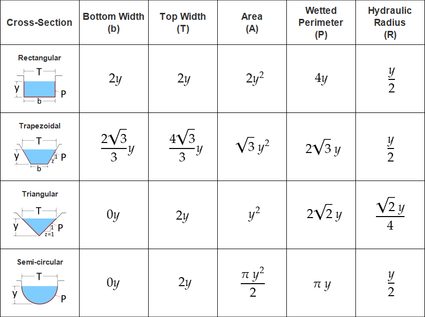
From the table above we'll see that the section with the lowest wetted perimeter $P$ is the semicircular section. To visualize this, imagine that we set the same arbitrary area $A$ of 4 m² for all cases shown. With this value, the flow depth $y$ and wetted perimeters $P$ are:

• Rectangular — $y =1.4142 \ \text{m}$ and $P=5.6569 \ \text{m}$;
• Trapezoidal — $y =1.5197 \ \text{m}$ and $P=5.2643 \ \text{m}$;
• Triangular — $y = 2\ \text{m}$ and $P=5.6569 \ \text{m}$; and
• Semi-circular — $y = 1.5958 \ \text{m}$ and $P=5.0133 \ \text{m}$.

From where the semi-circular section results with the lowest wetter perimeter. Nevertheless, these types of channels are the most difficult to build. That's why trapezoidal channels are the preferred shape. These are the next with the least wetted perimeter and are also simpler to build, making then the most efficient cross section for open channels.

If you'd like to learn more about trapezoids, how to calculate its area, perimeter and interior angles, you might find our trapezoid calculator useful.

Finally, when it comes to the slope of the channel, as mentioned, gravity is the main force that produces the movement of the fluid. It makes sense then that the steeper the channel the faster the fluid will flow.

Finally, as previously stated, gravity is the primary force that causes fluid flow, which makes the slope an important parameter to take into account. Therefore, the steeper the channel the faster the fluid will flow.

Manning's equation takes all of these aspects into account. This is an empirical equation used to estimate the velocity of a fluid through open channels or any other conduit that does not entirely enclose the fluid. Manning's equation for open channel flow is:

where:

• $V$ — Average velocity in m/s or ft/s;
• $k$ — Conversion factor between imperial and international units systems – $k =1$ for SI and $k=1.49$ for the imperial system.
• $n$ — Manning's roughness coefficient;
• $R$ — Hydraulic radius, given by the ratio between the cross-sectional area and perimeter of the channel –$R=A/P$; and
• $S$ — Slope of the channel's bottom surface.

The Hazen-Williams equation may be used to calculate gravity flow in pipes or enclosed conduits. You can also use the velocity $V$ to find the momentum of a certain volume of water, for example, with the momentum calculator if you know its weight.

From the velocity is possible to determine the volumetric flow rate Q of the fluid as:

where:

• $Q$ — Volumetric flow rate;
• $V$ — The calculated mass flow rate; and
• $A$ — Cross-sectional area of the water flow.

The open channel flow calculator can find the water flow rate and volumetric flow rate for custom-sized channels or the most economic cross-sections. In either case, all you have to do is:

1. Begin by selecting the type of design that you'd like to perform.
2. Proceed to enter the slope of the channel s.
3. From the Manning's coeff. (n) field, select the material of the channel's surface.
4. Enter the water flow depth y.
5. At this point, if you went for the most efficient design, the calculator will display your results.
6. If designing a custom channel, indicate the bottom b and top T width dimensions. The calculator will show you your results.