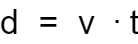Displacement Calculator

Use our displacement calculator if you need to know how to find displacement using different approaches. In the below text, we explain what displacement is, what the displacement vs. distance difference is, and how to get displacement from velocity and acceleration.

Displacement is a physical quantity that describes how far an object is from a certain point in a straight line. It's a vector as opposed to the distance, which is a scalar. The latter quantity is related to the total length of the path an object covered to get to the point.

We often use both terms interchangeably in ordinary language, so we decided to focus only on the scalar version of displacement, i.e., distance. Therefore, you can treat this tool as a distance and displacement calculator for which we use the same formula.

In case you need to know how to solve for displacement $d$ from various formulas, we prepared three methods in the displacement calculator:

1. How to find displacement using velocity $v$ and time $t$. Simply divide the former by the latter: $d = \frac{v}{t}$. Check our velocity calculator if you need to find this physical quantity instead of displacement.

2. How to get displacement using acceleration $a$ and time $t$. If you know acceleration and time or initial velocity $v_0$, final velocity $v_1$, and time, then this is how to solve for displacement using the mentioned quantities:

or

3. Total displacement formula using multiple velocities. Our total displacement calculator allows you to enter up to ten velocities ($v_1$, $v_2$, $...$, $v_{10}$). Be sure to also add the corresponding time ($t_1$, $t_2$, $...$, $t_{10}$) since in the total displacement calculator we use the weighted average where time is weight. In other words, we use the following formula:

4. That's all! The distance and displacement calculator also has the possibility to switch between units. In case of distance/displacement, you need to use length, usually meters or feet. The length converter on our site is a handy tool to convert any length units you want quickly and with no sweat.

The previous section explained how to get displacement in its scalar form, i.e., distance. What if you need to find actual displacement? Then you must use vectors! Let's see a simple example:

1. You have traveled from point $(0, 0)$ with a velocity of $v_1 = (0, 1)$ for $t_1 = 2$. That means you moved along the y-axis by two ending up at point $d_1 = v_1 \times t_1 = (0, 2)$.

2. Then the velocity changed to $v_2 = (1, 0)$ for $t_2 = 2$. This time you moved along the x-axis and the displacement change is now $d_2 = v_2 \times t_2 = (2, 0)$.

3. The total displacement formula says the total displacement is $d = d_1 + d_2 = (2, 2)$.

4. Eventually, the velocity changed to $v_3 = (-1, -1)$, again for $t_3 = 2$ so the displacement is $d_3 = v_3 \times t_3 = (-2, -2)$.

5. If you add all the partial displacements you will get $d = d_1 + d_2 + d_3 = 0$. So, you ended up at the starting point. Note that the distance is not zero in this situation but rather $4 + 2\sqrt{2} \approx 6.83$. To find the square root, use our root calculator to compute the nth radical of any positive number you want.