Free Fall Calculator

I wanna free fall out into nothin': John Mayer was wrong, and our free fall calculator will explain why you always free fall to the ground! Learn how to calculate how long and how fast an object falls to the ground!

With this handy tool, you will learn:

• What is free fall;
• The free fall equations in physics:
  • The free fall velocity formula;
  • The free fall time formula; and
  • How to calculate the coordinate of a falling object;
• Why does the weight doesn't affect the free fall acceleration;
• Examples of free fall: application of the free fall equations; and
• How to use our free fall calculator.

Free fall is a type of motion where a body is subjected solely to the gravitational pull of a bigger body (like a planet), with or without considering the friction force due to the air resistance.

Free fall has been the subject of one of the biggest mistreatment of science in human history: Aristotles affirmed that the speed of a falling object is proportional to its mass, and for centuries the strength of his ipse dixit prevented scientists from developing the correct theory of free fall.

Only in the 16^th century the first experiments on the matter started disproving the erroneous belief, and the final contribution of Galileo Galilei, with his famous experiment from the Leaning Tower of Pisa, settled the question for the years to come.

We will analyze only free fall in the absence of air resistance: this will make things way easier! Free fall is a situation where the only force acting on a body is gravity: the motion is hence uniformly accelerated.

If you need to consider the presence of air, head to our free fall with air resistance calculator.

To describe the motion of a falling object, we use the free fall equations. They are equivalent to the equations for a frictionless accelerated motion, substituting the value of $a$ with $g$.

To find the speed of a falling object (at the time $t$), we use the following free fall formula:

Where:

• $v_0$ is the initial velocity;
• $t$ is the time; and
• $g$ is the acceleration due to gravity.

You can compute the position of the falling object using this slightly more complex equation:

Where we introduced the vertical coordinate $y(t)$, and the initial height $y_0$.

The formula for the ** total time of a free fall** requires you to know only the initial height of the object in the best case. The same equation can be easily reversed to find the total distance traveled. In both cases, we assumed zero initial speed!

In the case of a non-zero initial speed, we find the total free fall time with the expression:

From these equations, we can find the final velocity of the fall:

Astronauts in orbit are not in an environment free of gravity as commonly though! The International Space Station, for example, is constantly free falling: the point is that it is traveling so fast that it misses the ground. Weightlessness is experienced in the same way you feel that "vacuum" after a bump on the road, just constantly.

Our free fall calculator implements the equations for the free fall in the absence of air resistance. You can calculate both the final parameters (final speed, total height, and total time) or the quantities at a given time, height, or speed.

Our tools work in any direction: don't follow the "direction" of the equation in the text, and insert any value you know. If you provide enough data, we will give you the answer!

How fast do objects fall? Now you know how to calculate it!

Let's consider an example: an object falling from the Leaning Tower of Pisa. The height of the platform you are using for your experiment is $y_0=48\ \text{m}$. Imagine you are dropping a $10\ \text{kg}$ lead sphere. What is the total time of the drop?

The final speed of the sphere, just before racing the ground is:

What if you dropped a weight with a tenth of the mass ($m=1\ \text{kg}$. Let's substitute the mass in the equatio- hey! The mass doesn't appear in any of the equations for a free fall! What does it mean?

In the absence of air, in the vacuum, the motion of a falling body is not affected by its mass. This is because the free fall acceleration remains constant and independent from the body itself; on the other hand, the gravitational force acting on it depends on the mass: the kinetic energy of an elephant falling in a vacuum is way higher than the one of a squirrel (which can survive any fall, thanks to its slow terminal velocity).

Galileo is said to have proved this concept by dropping weights with different masses from the Leaning Tower of Pisa; however, this is a likely anecdotal story!

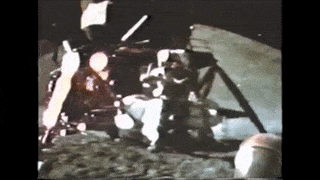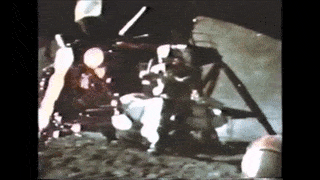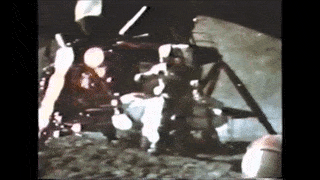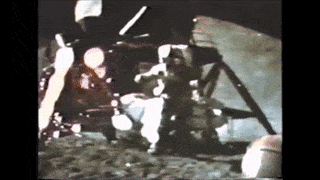
Anyway, due to the presence of air, only certain shapes of objects would be a good way to show the free fall independence from the mass. Lead spheres are ok but not quite impressive. That's why humans shot for the Moon to give a definitive demonstration. Literally!

David Scott, the commander of the mission Apollo 15, was recorded dropping at the same time a hammer and a feather (they couldn't go with a pair of more different objects). The two objects slowly (due to the reduced gravity) fell to the ground at the same time.