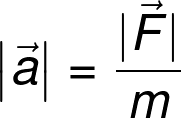Magnitude of Acceleration Calculator

How you calculate the magnitude of acceleration depends on the nature of your problem. Do you know velocity or force? With our handy tool, you will learn to tackle the problem in three different ways. Keep reading, or explore our calculator to learn:

• How to find the magnitude of acceleration given mass and force:
• How to find the magnitude of acceleration given velocity and time; and
• How to calculate the magnitude of the acceleration from its component.

We often use the terms speed and velocity interchangeably: we are wrong! In physics, speed is a scalar quantity, while velocity is a vector quantity. What's the difference? A scalar quantity is defined by a number, which quantifies the entity of the quantity. A vector quantity requires some additional elements:

• The orientation, the angle(s) defining the alignment of the vector (transversal, longitudinal);
• The sense, the way the vector is pointing (left/right, up/down); and
• The magnitude, the value inherited from the scalar quantities, indicates the "strength" of the vector.

Acceleration — the word, at least — is both a scalar and a vector quantity. We are interested in the second case.

We talk about acceleration in detail at our acceleration calculator. Check it out!

Acceleration is a versatile quantity: we can identify two main ways to calculate it. One involves newton's second law, which calculates it from a force using the famous equation $F = m\cdot a$. The other requires computing the difference between two vectors.

In our magnitude of an acceleration calculator, we will also teach you how to calculate the magnitude of acceleration using the acceleration's components.

Here we will learn how to determine the magnitude of the acceleration using Newton's second law.

Inverting the relationship, we can find the formula to calculate the magnitude of acceleration:

Where:

• $\left|\vec{a}\right|$ — The magnitude of the acceleration;
• $\left|\vec{F}\right|$ — The magnitude of the force (it corresponds to the absolute value of the force); and
• $m$ — The mass.

To find the magnitude of the acceleration in many problems regarding the motion of a body, you may need to know how to calculate this quantity starting from velocity and time.

To do so, you need to know:

• The initial and final velocity in vector form; and
• The time required to reach these values.

Once you know these values, compute the ratio between the calculated vector difference of the velocities and the time:

Where:

• $\vec{v}_\text i$ — The initial velocity;
• $\vec{v}_\text f$ — The final velocity; and
• $\Delta t$ — The time.

To compute the subtraction between the velocity vectors, follow these steps:

1. Subtract individually the components for each coordinate;
2. Sum the squares of the results;
3. Extract the square root of the result.

Remember to convert the speed into a reasonable measurement unit before calculating the acceleration: Beaufort per second square is not a good unit. Check our speed converter if you need help!

Since acceleration is a vector quantity, we can define as many components as the number of dimensions of the space we are working in. A projection is the orthogonal projection of the vector on a given axis. For a two-dimensional space we have two components, usually the $x$ and $y$ one. We represent the acceleration vector as:

To compute the magnitude of the acceleration in this situation, apply the formula:

You can arbitrarily increase the number of dimensions and components to fit the requirements of your problem. In the general case, the equation for the magnitude of the acceleration is: