Wind Correction Angle Calculator

Our wind correction angle calculator is here to help you determine the adjustments to your aircraft's course to offset the effects of the wind. In this article, we shall discuss the basics of wind correction angle calculation, including:

• Effects of wind on an aircraft flight path.
• Vector analysis and wind correction formula.
• Calculating true heading.

Another useful tool is the wind load calculator, which finds the force that winds exert over structures. Be sure to check it!

The wind correction angle (WCA) is the angle between the aircraft's heading and the actual direction of travel. We use it to compensate for the effects of wind on the aircraft's flight path. The wind correction angle is critical because it helps to keep the plane flying in the correct direction. Without it, the aircraft would be blown off course by the wind.

Weather forecast contains information about wind speed (WS) and direction at different altitudes. Pilots are constantly monitoring the weather forecast to calculate the WCA for each leg of the journey and adjust the plane's heading as necessary.

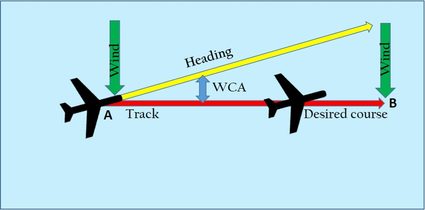
The aircraft's speed and weight also affect the wind correction angle. A faster, heavier aircraft will need a larger correction angle than a slower, lighter aircraft.

Consider the following vector diagram:

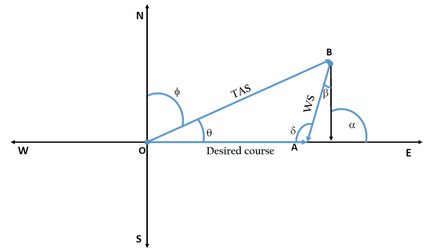
The different vectors and angles are explained below:

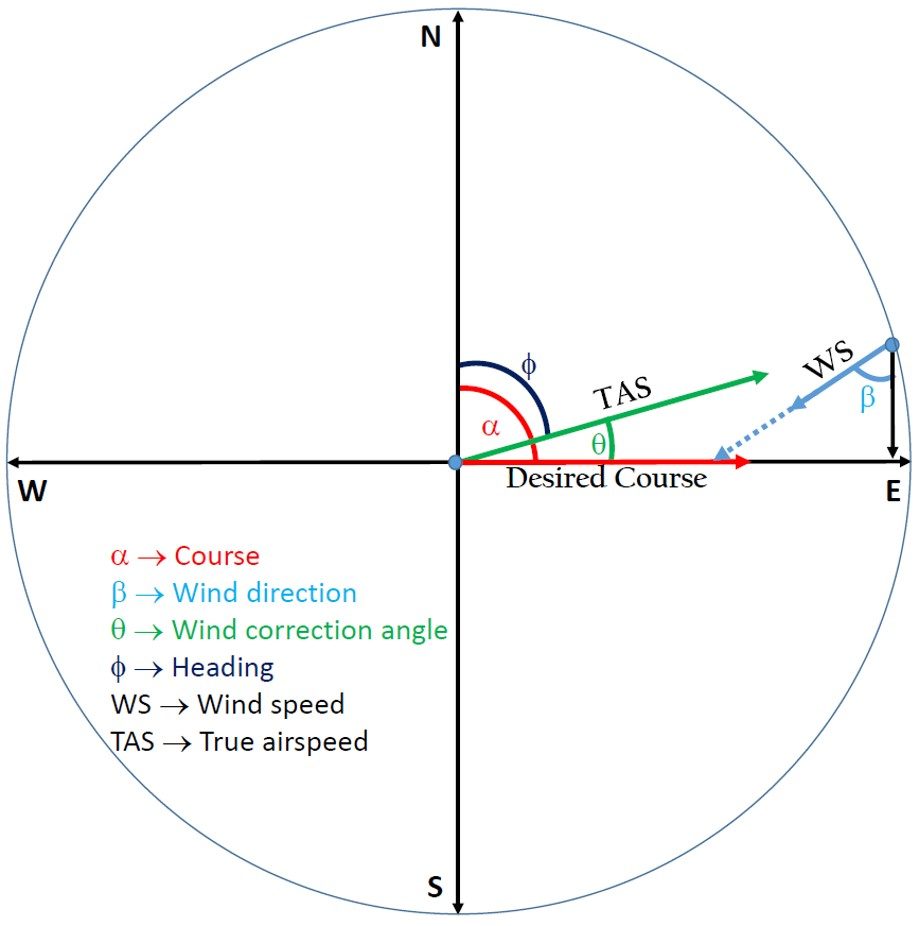
• $\overrightarrow{OA}$ represents the desired course direction. $\alpha$ is the angle between the true north and desired course (measured clockwise).

• $\overrightarrow{BA}$ represents the wind speed $(\text{WS})$. $\beta$ gives the direction from which the wind is blowing. Measure the angle between the wind direction and true south.

• $\overrightarrow{OB}$ represents the true airspeed $(\text{TAS})$. $\phi$ is the angle between true north and the aircraft heading.

• $\delta$ is the angle between the wind direction and the desired course, given by: $\delta = \alpha - (180\degree + \beta)$.

• $\theta$ is the wind correction angle.

Using the law of sines on $\triangle \text{OBA}$, we get the formula for wind correction angle:

If you need help finding the sine values for different angles, our trigonometric functions calculator is here to help.

To calculate the true course (or true heading) $\phi$, we must subtract the calculated wind correction angle $\theta$ from the desired course $\alpha$:

Our wind correction angle calculator is simple to use:

• Enter the aircraft's true airspeed and the desired course$(\alpha)$.
• Provide the wind speed and wind direction $(\beta)$.
• The calculator will automatically determine the wind correction angle $(\theta)$.
• It will also calculate the true course or heading of the aircraft.

A similar calculator you can explore here at Calctool is the ground speed calculator.