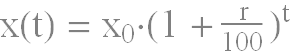Exponential Growth Calculator

Welcome to our exponential growth calculator, a powerful tool to determine the exponential increase in quantity over time. You can also use it to calculate the exponential decay - the exponential decrease in quantity over time! Read through this article to learn about the exponential growth function and exponential growth formula.

Exponential growth is the increase in quantity over time such that the change is exponential in nature. The formula for exponential growth is:

where:

• $x(t)$ - The quantity as a function of time (at time $t$);
• $x_0$ - The initial value of the quantity (at time $t_0$); and
• $r$ - The growth rate (or rate of change).

Note that we assume the rate of change is a constant. Since the time variable $t$ is an exponent over the rate of change $r$, we can surmise that the change in quantity will be drastic over extended periods, far greater than linear and polynomial growth.

We can use Logarithm to find the time $t$ if the other parameters are known.

A town with a population of 5000 grows steadily at $6\%$. Let's use the exponential growth equation to find the population after 3, 6, 9,12, and 15 years.

Substituting the initial value of 5000 and the growth rate of 6%, we get:

Now let's evaluate this population growth formula for the different periods and tabulate it.

Try calculating the same problem with a $10\%$ growth rate. For greater growth rates, you will notice a steeper increase over time.

The exponential growth rate helps calculate the population growth of bacteria, viruses, plants, and animals. Hence, the population growth formula can use the exponential growth model. We also use exponential growth models to calculate the air pressure at different altitudes and compound interest.

Now that you know how to calculate exponential growth let's focus on exponential decay.

Exponential decay is a decrease in quantity over time. The formula for exponential decay is:

In other words, we can calculate exponential decay using the exponential growth equation, but with a negative rate of change.

This exponential growth calculator is a versatile tool that is easy to use:

• Enter the initial value $x_0$.
• Provide the rate of change $r$. For calculating exponential growth, the rate must be positive. For calculating exponential decay, the growth must be negative.
• Enter the elapsed time $t$. Note that you can use a negative time to find the value at an earlier time.
• This exponential growth calculator will automatically calculate the final value $x(t)$.

This calculator can function backward! Enter any three known values in any order to find the remaining unknown.