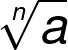Root Calculator

Welcome to our root calculator, a simple tool to calculate the nth root of any real number. Whether you want to calculate square root or fourth root, our nth root calculator has you covered. In this article, we shall discuss the nth root and how to calculate it, so keep scrolling and find out more.

The nth root of a real number a is the number we must raise to the power n to produce a. Mathematically, we express this as:

Where $x$, $n$ and $a$ are all real numbers. $x$ is the nth root of $a$.

For example, the 4 is the 3rd root of the number 64, because $4 \times 4 \times 4 = 64$.

The 2nd root of a number is so common that it has its unique name - square root. One method to find the square root of a number involves prime factorizing the number and looking for pairs of primes. Consider the number 81.

1. Prime factorize 81 to get:

2. Look for pairs of primes. We can gather two pairs of 3s:

3. Apply the square root. For each pair, we shall get one prime out of the square root.

4. Multiply the remaining numbers together to get the answer:

5. Verify this result with our root calculator, which can also function as a square root calculator!

We use square roots everywhere, especially in geometry. Find out its crucial role in determining one side of a right triangle from the other two sides using our Pythagorean theorem calculator.

Calculating the nth root is similar to calculating a square root. The only change after prime factorization is we must look for groups of n primes instead of 2. For example, calculating the fourth root of 81 will give us:

Notice that calculating the fourth root of a number is the same as finding the square root of the square root of the number!

This nth root calculator is straightforward to use:

• Enter the number a for which you seek the nth root.
• Enter the value of n.
• Our root calculator will automatically display the nth root of the number a.
• To use it as a square root calculator, enter 2 as the value for n.