Focal Length Calculator

Our focal length calculator will help you figure out the focal length needed to capture a distant object through a thin lens. It will also calculate the magnification and field of view of the lens. This article will teach you the focal length equation and image distance formula. Additionally, you will learn how to calculate the field of view and magnification using focal length. So hop in!

If you're interested in learning how a lens is made for a given focal length using materials of different refractive indices, visit our lensmaker equation calculator without fail!

The focal length of a lens measures how sharply it can bend the light rays to converge at or diverge from a focal point. It is the distance between the center of the lens and the point where the light rays converge or diverge.

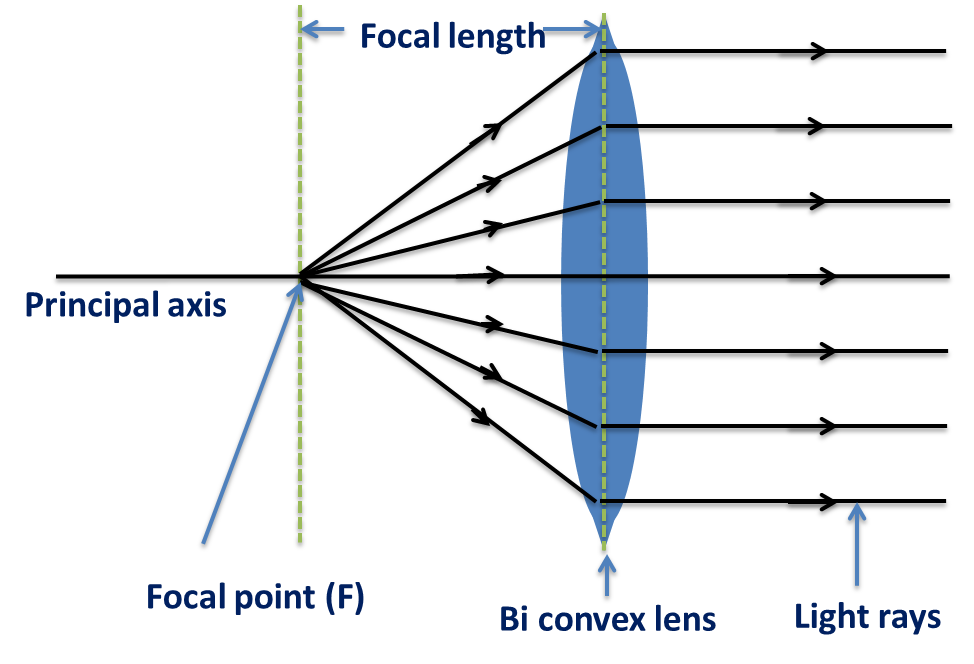
The formula for the focal length of a thin lens is:

Where:

• $f$ - Focal length of the lens;
• $u$ - Distance from the object to the center of the lens (also known as object distance); and
• $v$ - Distance from the image to the center of the lens (also known as image distance).

For more, visit our thin lens equation calculator calculator.

For a converging lens, it is common practice to form a sharp image of a distant light source on a screen. Since the object (light source) is far away, $\frac{1}{u}$ becomes negligible, and the focal length is approximately equal to the image distance.

In photography, it is desirable to eliminate the parameter image distance from the focal length equation by introducing the magnification of the image.

Magnification $M$ refers to the enlargement or contraction of the image size compared to the object size. It is given by:

Magnification is also related to the focal length and object distance by the following equation:

Rewriting this equation will give us the formula for focal length in terms of object distance and magnification:

The field of view or angle of view refers to how much of the scenery can be captured by the lens. Wide angle lenses and ultrawide cameras are becoming household names thanks to many smartphones.

We can calculate the field of view $\text{FoV}$ of a lens from its focal length using the equation:

Our focal length calculator is an amateur photographer's best friend:

• To calculate the focal length of your sensor:
  • Enter the object distance and the image's magnification.
  • Provide the object size to find out the image size.
• To calculate the magnification, enter the sizes of the image and object, or provide the object distance and focal length.
• To calculate the field of view of your lens:
  • Enter the focal length of the lens along with the image size and magnification.
  • Alternatively, provide the focal length, image size, and object size.

If you're interested in more optical calculations, check out our mirror equation calculator.