Malus Law Calculator

Our Malus' law calculator is here to help you calculate the light intensity when it passes through a polariser. If you're curious about how the intensity of light changes as you turn your camera's polariser, you've come to the right place! In this article, we shall go through some fundamentals of polarised light intensity, including:

• Malus' law and light polarization.
• Malus' law formula.
• How to calculate the intensity of polarized light.

Remember to check the mirror equation calculator if you need to analyze the path of light in concave, convex, or planar mirrors.

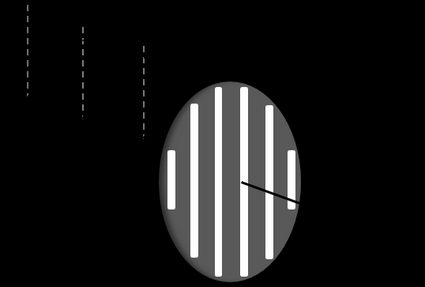
Malus' law states that the intensity of polarised light passing through a perfect polariser is proportional to the cosine of the angle between the axis of the polariser and the initial light's polarisation. We can write the Malus law equation as:

Where:

• $I$ - Intensity of light after passing through the polariser, in Watts per meter square $\text{W/m}^2$;
• $I_0$ - Intensity of light before passing through the polariser, in Watts per meter square $\text{W/m}^2$; and
• $\theta_i$ - Angle between the polariser's axis and the light's initial polarization.

Our other tool, the distance attenuation calculator, focuses on finding the intensity of sound over a certain distance. Be sure to check it as well!

Let's understand Malus' law better with some examples:

1. Consider a polarised light with only vertical polarization. Calculate the light intensity when it passes through a polariser oriented $30 \degree$ to the vertical if the initial intensity was $4 \text{ W/m}^2$.

Given:

• Initial intensity $I_0 = 4 \text{ W/m}^2$.
• Angle between the polariser's axis and the light polarization $\theta_i = 30 \degree$.

To find:

• Final intensity $I$.

Let's calculate the light intensity equation from Malus' law:

2. By what angle must we orient the polariser in the previous example to reduce the intensity to $1 \text{ W/m}^2$?

Given:

• Initial intensity $I_0 = 4 \text{ W/m}^2$.
• Final intensity $I = 1\text{ W/m}^2$.

To find:

• Angle of polariser.

Rewriting the Malus' law formula:

Our Malus' law calculator is simple to use:

• Enter the initial intensity of the polarised light before passing through the polariser.
• Provide the angle between the polariser's axis and the light's initial polarization.
• This calculator will instantly determine the final light intensity after it passes through the polariser.
• You can also reverse this Malus' law calculator to solve problems like the second example in the previous section!

Had fun playing with Malus' law and polarized light? Check out our Brewster angle calculator for more on polarized light!