Elevation Grade Calculator
With our elevation grade calculator, you can easily find the angle of elevation of an area of land.
Within this short text, you will learn what the angle of elevation is and how to calculate elevation between two points.
Keep reading to learn more!
What is the elevation grade or angle of elevation?
Commonly known as:
- Angle of elevation;
- Elevation grade;
- Slope; or
- Stepness
the angle of elevation measures how steep an area of land is and has many applications. Land surveyors and engineers widely use it in different scenarios such as construction or finding out the amount of needed to move an object.
We can also use it to calculate the height of a distant object, knowing its horizontal distance to a point. How? Let's see how to find the elevation grade first. Then we'll do some examples with the elevation grade calculator.
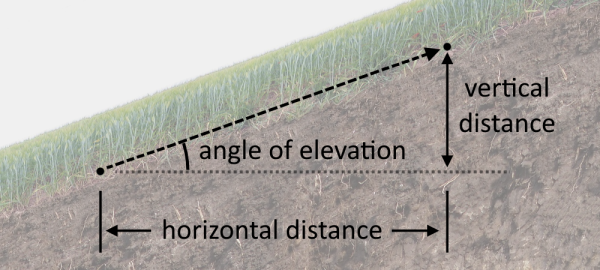
How to calculate elevation between two points
Finding the elevation grade is similar to finding the slope or rate of change between two points. For that, we need two things:
- The vertical distance between the points or "rise"; and
- The horizontal distance between the points or "run".
That way, we can express the elevation grade in terms of the rise over run quotient (rise/run), or angles according to these formulas:
Our elevation angle calculator outputs both results for you to choose from!
Example finding the elevation grade
Assume we know that the distance between two pieces of land is:
- ; and
- .
Then, we can replace these parameters in the elevation grade formula to find:
As you see, the calculation is straightforward! Feel free to start experimenting with our calculator 📐.
How to find height based on distance and elevation grade
You can use the elevation grade calculator to find the height of a distant object. The angle of elevation, in this case, is the angle between the top of the object and our position.
Suppose we have:
- , the distance to the unknown height object; and
- , elevation grade or angle of elevation in degrees.
If you want to find the height manually, all you need to do is multiply the tangent of the angle of elevation by the horizontal distance or run.
Else, using our tool, we input and in the "Horizontal distance" and "Angle of elevation" fields, respectively.
Lastly, the elevation grade calculator will automatically fill the "Vertical distance" field, which is the object's height!