Centrifugal Force Calculator

Rotational motion is present in many real-life situations, such as the movement of centrifugal pumps, car engines, orbital period formula, or the tagada of amusement parks; for that reason, we created this centrifugal force calculator.

In the following section, we talk about:

• The definition of centrifugal force.
• The acceleration and centrifugal force formulas.
• The equation for centrifugal force calculation, with velocity in rpm instead of rad/s.

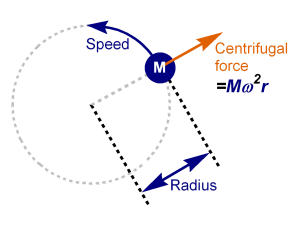
Centrifugal force is the fictitious or inertial force that a rotating object feels. We consider it fictitious because it only appears in non-inertial frames of reference, while the observers in an inertial reference frame don't perceive it.

Understanding the centrifugal acceleration is necessary to know where the centrifugal force formula comes from.

The centrifugal acceleration formula is:

where:

• $a$ — centrifugal acceleration (m/s²);
• $\omega$ — angular speed (m/s); and
• $r$ — radial distance to the axis of rotation (m).

We can also express the centrifugal acceleration formula in terms of the tangential velocity $v$:

The equation for centrifugal force comes from the definition of force, which says it equals mass times acceleration. Multiplying mass by angular acceleration, we have:

where:

• $F$ — Centrifugal force, usually expressed in newtons (check the Omni's force converter for more information about force units);
• $m$ — Mass of the object;
• $\omega$ — Angular velocity
• $r$ — Radial distance to the axis of rotation.

As with centrifugal acceleration, we can express the centrifugal force equation in terms of tangential speed:

Since the centrifugal force is strictly related to the rotational motion, you may want to express the coordinates with a more convenient system. Check our cartesian to polar coordinates calculator to see the latter method's advantages.

Sometimes we need to calculate the centrifugal force, but we possess the angular velocity in rpm instead of rad/s. Instead of converting from rad/s to rpm, we can develop a centrifugal force formula for rpm inputs:

First, let's remember the relationship between rad/s to rpm.

Considering the previous relationship, we can calculate the centrifugal force (using rev/min) with the following formula:

In the previous formula, $RPM$ is the angular velocity in revolutions per minute.