Heat Transfer Coefficient Calculator

Use this heat transfer coefficient calculator the determine the overall heat transfer coefficient $U$ for plane surfaces. From the design of a building's insulation, refrigeration systems, the cooling system of electronic components to heat exchangers in the oil industry, different heat transfer mechanisms such as conduction, convection, and radiation take place. The overall heat transfer coefficient $U$ allow us to study all of them as one single number, making it easier to calculate the heat transfer rate in these and other applications.

Keep on reading to learn:

• What the overall heat transfer is;
• How it combines the effects of convection and conduction;
• The electrical resistance and thermal resistance analogy; and
• The overall heat transfer coefficient formula.

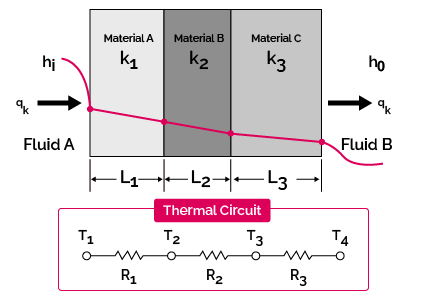
In applications such as wall and roof insulation or heat exchangers, heat transfer is associated with the combined effect of the convection and conduction mechanisms. For instance, in an insulated wall where the outside temperature is higher than the inside temperature, the heat moves from the outside air, through the bricks and other layered solid materials that form the walls, to the inner side air.

In the case of heat exchangers, the heat transfer occurs between the fluids separated by a wall, i.e., a pipe. Here, heat is transferred from the hot fluid to the wall by convection, then through the wall by conduction, and finally from the wall to the cold fluid again via convection.

We can calculate the heat transfer rate of such arrangements using the overall heat transfer coefficient $U$, as shown in the following formula:

Where:

• $\dot{Q}$ – Heat transfer rate;
• $U$ – Overall heat transfer coefficient;
• $A$ – Heat transfer surface; and
• $\Delta T$ – Temperature difference.

The overall heat transfer rate $U$ comes in units of energy per unit of area and temperature, as $\text{W/m}^2\text{⋅K}$ or $\text{BTU}/(\text{h ⋅°F ⋅ ft}^2)$.

Note from this equation that since heat is directly proportional to the overall heat transfer coefficient $U$, lower values of $U$ translate into lower values of $\dot{Q}$ and vice versa. This idea is applied in building insulation, where we can use low values of $U$ to achieve a low heat transfer between the outside and the inside.

Before we drop the overall heat transfer coefficient $U$ formula, let's first consider the electrical resistance analogy. From electric circuits, we can recall that it's possible to relate the circuit's current, voltage difference, and electrical resistance with Ohm's law:

Where:

• $I$ – Current flow;
• $V_1 - V_2$ – Voltage difference; and
• $R_\text{e}$ – Electrical resistance.

Notice that the electrical resistance is inversely proportional to the current. As you might expect, the higher the values of $R_\text{e}$, the more difficult it'll be the movement of the current. In other words, given the same voltage difference, we can expect lower values of $I$ as $R_\text{e}$ increases.

In heat transfer, we find an analogous relationship, where instead of evaluating the current flow, we study the heat transfer rate $\dot{Q}$. We know there're materials through which heat transfer is easier than in others. For the analogy, we call this property the thermal resistance $R_\text{t}$. And instead of voltage difference, we talk about temperature difference $\Delta T$. We can identify these terms from the heat rate formula above-mentioned:

Here we can instantly identify $\dot{Q}$ and $\Delta T$. To complete the electrical resistance analogy, we need to define the thermal resistance $R_\text{t}$ as:

Then the heat transfer rate can be expressed as:

How can we determine the thermal resistance $R_\text{t}$? For conduction for plane walls, we calculate it as:

Here, $L$ represents the thickness of the wall and $k$ its thermal conductivity. For several layers stacked one after another, each of the materials have its own properties, and we can generalize the thermal resistance equation as:

Where $L_i$ is the thickness of each wall layer and $k_i$ is the respective conductivity.

When we incorporate the convection effect, we use the convective heat transfer coefficient $h$, and the corresponding thermal resistance is:

In this calculator, we're studying scenarios like the one depicted in the image, where heat travels from the inside air, through each wall's layers, to the outside air. By adding the convective resistance to the conductive resistance, we get a total thermal resistance for multilayered plane walls:

Where:

• $h_i$ – Convective heat transfer coefficient of fluid, inner surface; and
• $h_o$ – Convective heat transfer coefficient of fluid, outer surface.

The values for the convective heat transfer coefficient of air are usually between 10 to 100 $\text{W/m}^2\text{⋅K}$.

Since the heat transfer surface is the same $(A_i=A=A_o)$, we can take it out as a common factor and place it on the left side of the equation, multiplying the thermal resistance and obtaining an equation for the overall heat transfer coefficient $U$:

This is the overall heat transfer coefficient formula $U$:

Now that you know how to calculate the heat transfer coefficient $U$, you might want to learn how to find the temperature difference $\Delta T$ for heat exchangers 🔥 If this is your case, then you should take a look at the log mean temperature calculator LMTD.

With the heat transfer coefficient calculator, you can determine the overall heat transfer coefficient and the thermal resistance of a plane wall system of up to 10 layers. This tool works in two modalities, conduction only and conduction and convection. Let's see how to use this tool for each case:

Conduction only

1. Begin by selecting the Conduction only option on the Mode section of the calculator.
2. Enter the value of the heat transfer Area.
3. In the Initial thickness section, select the Material and input its Thickness (L0). For custom materials, manually enter the value for its Thermal conductivity (k0).
4. At this point, the calculator will already have results for this initial configuration. However, if you need to include more layers of materials, you can do so by using the Add option.
5. Repeat instructions from step 3 for each extra layer you include.
6. Once you have finished defining each layer, the calculator will show you the results for Overall heat transfer coefficient (U) and Thermal resistance (Rt).

Conduction and convection

1. Select the Conduction and Convection (on both sides) option on the Mode field of the calculator.
2. Input the Area of contact.
3. Insert the convective heat transfer coefficient associated with the inner surface, Convective heat transfer coefficient, inner (Hi).
4. In the Initial thickness section, choose the Material and indicate its Thickness (L0). For custom materials, you'll need to manually enter its Thermal conductivity (k0).
5. To include another layer, use the Add option. You can incorporate up to 10 layers!
6. Repeat instructions from step 4 for each extra layer.
7. Once all the layers are defined, enter the convective heat transfer coefficient of the outer surface, Convective heat transfer coefficient, outer (Ho).
8. Finally, the calculator will display the Overall heat transfer coefficient (U) and Thermal resistance (Rt) for your configuration.