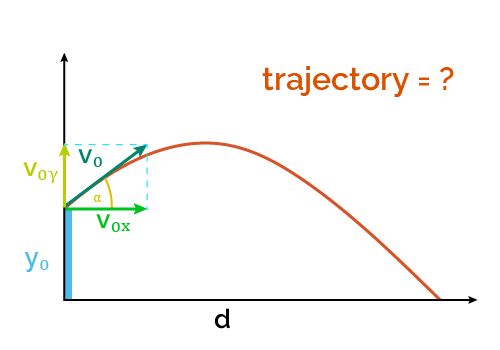
Trajectory Calculator
Welcome to our trajectory calculator, where you'll be able to find the projectile motion given the angle of trajectory, initial height, and initial velocity (or simply, speed).
This calculator focuses on finding the whole trajectory of a projectile using the trajectory formula and gives you the vertical position as a function of the horizontal .
Trajectory formula
The formula with which this tool calculates the trajectory of a projectile is:
where:
- — Initial projectile height;
- — Horizontal component of the projectile position;
- — Projectile height (vertical position) at a specific horizontal distance ;
- — Angle of launch (initial angle of trajectory);
- — Gravity acceleration; and
- — Launch velocity.
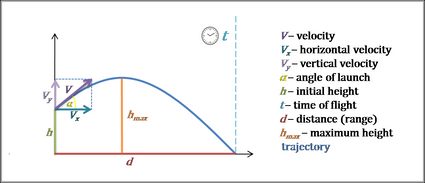
As you can note, this is a vertical distance formula in terms of the horizontal distance .
Trajectory formula derivation
Where does the vertical distance formula come from?
-
First, let's remember the equations of motion for the horizontal () and vertical () positions:
-
As the launch velocity () and its horizontal and vertical components ( and ) form a right triangle, we can say:
-
Now, let's solve for in the equation and express it in terms of :
- →
-
Replacing and in the equation:
-
As , then:
That's it! We've derived the trajectory formula.
How to use this trajectory calculator?
Imagine you have the parabolic water jet of the following image and want to calculate its trajectory.

Suppose the launch velocity of the water jet is 2 m/s, with a 50° angle and an initial height of 5 cm. Follow these steps to calculate the trajectory:
- Input 0.5 m/s in the "Velocity" box.
- For "Angle of launch," input 50 deg.
- In the "Initial height" box, select cm as the length unit and input 5 cm.
- That's it! The trajectory calculator should show you a plot with the height as a function of horizontal displacement, representing the projectile motion.
The trajectory of projectile motion is a simple quadratic relationship between height and distance. You can analyze this kind of curve and determine its features with the polynomial graph calculator.