Polynomial Graphing Calculator

If you were searching for a tool to generate polynomials graphs, this polynomial graphing calculator is what you need!

In addition, you can also use this polynomial grapher calculator to determine features of polynomial graphs, such as:

• The real roots of the polynomial.
• The critical points.
• The local extrema.
• Inflection points.

Polynomials are algebraic expressions in which variables appear only in non-negative integer powers. Therefore, the letters cannot be, e.g., under roots, in the denominator of a rational expression, or inside a function. Generating polynomial graphs manually often requires knowing two features of the polynomial:

1. Polynomial roots

The root or zero of a polynomial is a point in the domain (x-values) where a function equals zero. For example, the polynomial P(x) = 2x² - 2x - 12 has a zero in x = 3 since:

P(1) = 2*3² - 2*3 - 12 = 18 - 6 - 12 = 0.

Finding the root is simple for linear equations (first-degree polynomials) and quadratic equations (second-degree polynomials), but for third and fourth-degree polynomials, it can be more complicated. There are formulas for polynomials of third and fourth-degree, but they are long and require tedious work.

2. Critical points

Critical points are the next step in drawing a polynomial graph. They describe the graph behavior between the roots: if the values increase or decrease, and until what number they do it. At critical points, the derivative of the polynomial equals zero.

There are two types of critical points:

1. Local extrema: points of the polynomial around which all other values are smaller or larger. These are also known as the maxima and minima of a function.
2. Inflection points: When a graph approaches its inflection point, it flattens as if it were a local extrema, but without changing the course once it passes. Instead, it repeats what it was doing: decreases if it was decreasing or increases if it was increasing.

Apart from graphing polynomials, you can also use this polynomial graphing calculator to find the zeros of polynomial functions and calculate other features. Let's see, through an example, how to do it.

Suppose we want to generate the graph of the polynomial P(x) = x⁴ - 2x. Follow these steps to get the answer:

1. Identify the polynomial degree and input it into the polynomial grapher. In this example, select 4 as the polynomial degree.
2. Identify the value of the coefficients of the polynomial. In this case:
   • a₄ = 1
   • a₃ = 0
   • a₂ = 0
   • a₁ = -2
   • a₀ = 0
3. Input the coefficients in the polynomial graphing calculator.
4. That's it! The calculator should generate this polynomial graph:

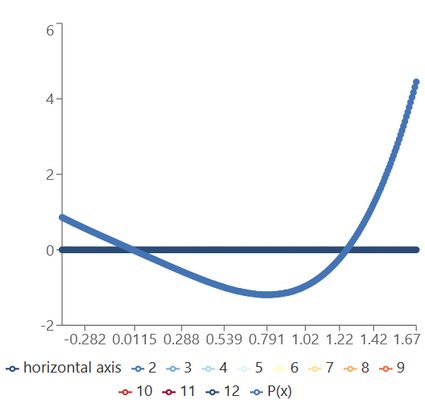
Additionally, for this case, the calculator determines these features of the polynomial graph:

• Two real roots, at points 1.25992 and 0.
• A critical point at 0.7937.
• An extremum at 0.7937 (minimum with value -1.19).
• No inflection points.