Section Modulus Calculator
Calculating the section modulus is an interesting way to study the stress response of a beam to bending. With this tool, you'll be able to calculate the elastic and plastic section modulus of I-sections and many other common structural shapes.
If you don't know what is the section modulus, in the following article, we talk about it, the difference between the elastic and the plastic version, and the formulas for its calculation. Keep reading!
What is the elastic section modulus?
To know where the section modulus comes from, let's remember the widely known flexure formula used to determine the maximum stress in a beam subjected to bending:
where:
- — Maximum normal stress in the beam. This stress occurs at a distance from the neutral axis.
- — Largest perpendicular distance from the neutral axis to a point in the section;
- — Bending moment about the neutral axis; and
- — Area moment of inertia of the beam cross-section about the neutral axis.
Let's remember that this equation only applies if the beam meets the following conditions:
- It is a prismatic beam (i.e., in the form of rectangular prism).
- It is symmetrical about the axis perpendicular to the neutral axis.
- Its material is homogenous and behaves according to Hooke's law.
For example, we can use the flexure formula for the following case:
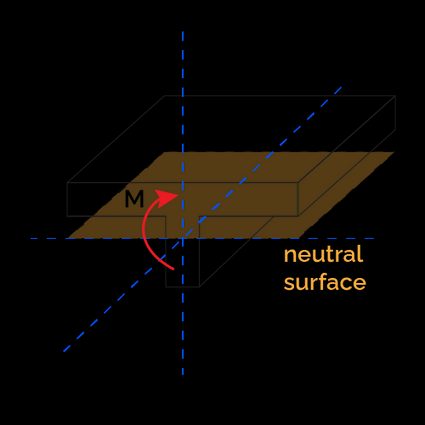
Just like the area moment of inertia, the distance depends solely on the geometry of the section. We can combine and and generate a new geometrical property that entirely accounts for the effects of the geometry on the normal stress. This property is known as the section modulus or elastic section modulus:
With this new property, we can now calculate the maximum normal stress due to bending by only knowing and :
As well as for the moment of inertia, we can define the section modulus for the x and y directions. The axis to choose will depend on the direction of the momentum vector. For example, if the moment vector acts in the x-direction (the most common situation), we choose the section modulus in the x-direction.
Even so, if we face the situation of unsymmetric bending (bending in various directions or planes), we'll need to use methods that require the section modulus in both directions. In the last section of this article, you can look at a table with the different elastic and plastic section modulus formulas for different axes.
What is the plastic section modulus?
The plastic section modulus has a similar function to its elastic counterpart, but for situations in which we surpass the yield strength of the material and it no more exhibits a linear elastic behavior. The elastic section modulus makes it possible to calculate the plastic moment of the section:
where:
- — Plastic moment;
- — Plastic section modulus; and
- — Yield strength of the beam material.
The plastic moment refers to the moment required to cause a plastic deformation across all the fibers of the beam section. As we know, for bending, the normal stress is higher at the points farthest from the neutral axis, and, therefore, it will reach the yield strength first at those points. Once the moment (M) equals the plastic moment (Mp), the yield strength will have reached the whole section.
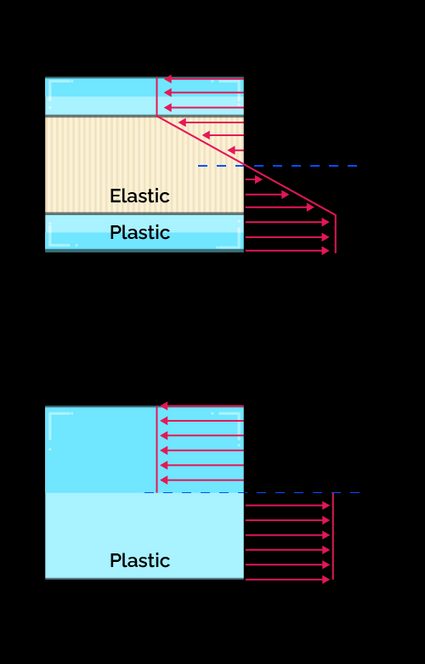
With the previous equation, we can easily predict the bending moment that will cause plastic deformation by only knowing the plastic section modulus and yield strength.
Now that we know the concepts let's look at the different formulas to calculate the section modulus.
Formulas to calculate the section modulus
In the following table, you can look a the elastic and plastic section modulus formulas, which are the ones this section modulus calculator uses. Scroll sideways to display the whole table.
Form | Elastic section modulus (S) | Plastic section modulus (Z) | |
|---|---|---|---|
Square | 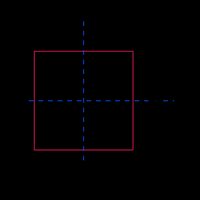 |
|
|
| |||
| |||
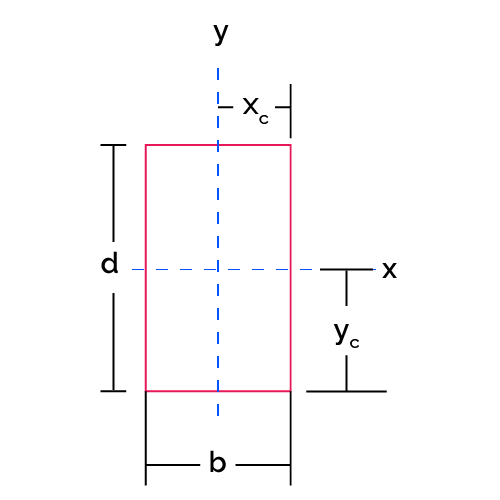
Rectangle | 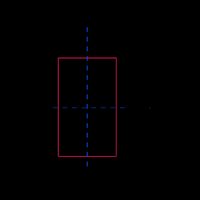 |
|
|
|
| ||
| |||
| |||
| |||
| |||
Hollow rectangle | 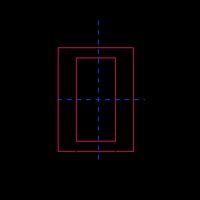 |
|
|
|
| ||
| |||
| |||
| |||
| |||
Tee section |  |
| If , then |
|
| ||
| If , then | ||
|
| ||
|
| ||
| |||
| |||
Channel section | 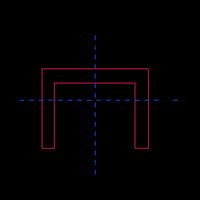 |
| If , then |
|
| ||
| If , then | ||
|
| ||
|
| ||
| |||
Wide-flange beam (equal flanges) | 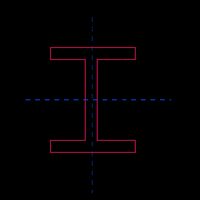 |
|
|
|
| ||
| |||
| |||
| |||
| |||
Angle |  |
| If , then |
|
| ||
| If , then | ||
|
| ||
| |||
| If | ||
|
| ||
If | |||
| |||
Circle | 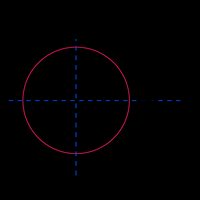 |
|
|
| |||
| |||
Hollow circle | 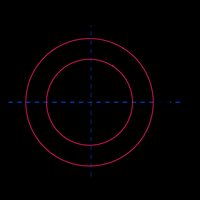 |
|
|
| |||
| |||