Beam Shear Stress Calculator
Welcome to this shear stress calculator, a tool created to:
- Calculate the shear stress in a beam due to a transverse shear; or
- Calculate the shear stress in a circular shaft due to a torsional load.
Obtaining the variables of the transverse shear stress equation (𝜏 = VQ/It) is usually an uphill task. For that reason, we also included some special cases, such as the transverse shear of rectangular, circular, and I-beams.
According to your needs, this calculator also can provide its results in different shear stress units, such as Pascals (Pa), kilopascals (kPa), megapascals (MPa), psi, and ksi.
If you want to learn more, in the rest of this article, we present the shear stress equations used by this calculator.
Shear stress
Opposite to the axial stress we saw in our stress calculator, shear stress acts tangent to an area. Although the determination of axial stress is usually easy (σ = F/A), shear stress involves more complexity, especially the one caused by transverse loads.
Transverse shear stress formula
In a beam subjected to transverse shear, the shear stress varies with vertical distance. For example, the stress is not the same at the beam center as at the upper or lower extremes.
You can calculate the shear stress in the beam at any point using the following equation:
, where:
- — Beam Shear stress calculated at a point at a specific vertical distance from the neutral axis.
- — Internal shear force at the section of interest in the beam. It is the one we calculate using the method of sections and equations of equilibrium.
- — First moment of area of the portion above the point where we'll calculate the stress, where:
- — Area of the portion above the point where we want to calculate the stress; and
- — Distance from the centroid of to the neutral axis of the whole beam.
- — Section width at the point where we'll calculate the shear stress.
- — Second moment of area of the entire beam cross-section, about the neutral axis (the one we also use for bending stress). You can obtain it with our moment of inertia calculator).
As an image is worth a thousand words, in the following image, you can figure out what we mean by , , and when calculating the shear stress at a point at a distance from the neutral axis (NA)

Rectangular, circular and I-beam sections
In the following table, you can look at the shear stress formulas used for the special cases of the calculator. If the cross-sectional area is solid instead of hollow, let .
Form | Maximum shear stress | |
|---|---|---|
Rectangle | 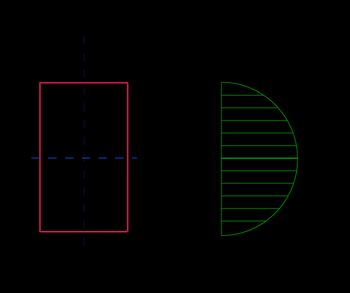 |
|
| ||
Stress at distance y: | ||
| ||
Hollow circle | 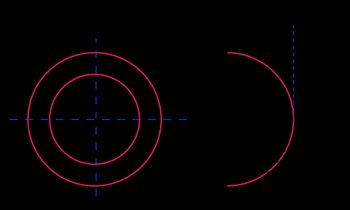 |
|
| ||
I-beam | 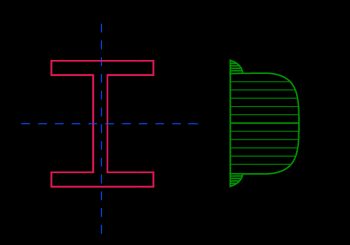 |
|
| ||
| ||
Torsional shear stress equation
In a circular member subjected to torsion, the shear stress varies radially across the cross-section. To calculate the shear stress in a beam of circular section (usually known as a shaft) subjected to torsion, we use the following formula:
, where:
- — Shear stress at a radial distance from the center;
- — Polar moment of inertia of the shaft cross-section; and
- — Internal torque at the section of interest in the shaft (the one we calculate using the method of sections and equations of equilibrium).
We can note from the formula that the maximum shear stress () in this type of load occurs at the outer surface, where
Where is the shaft radius.
The two shear stress formulas above apply for solid and hollow shafts, differing only in how we calculate the polar moment. To obtain , visit our polar moment of area calculator.
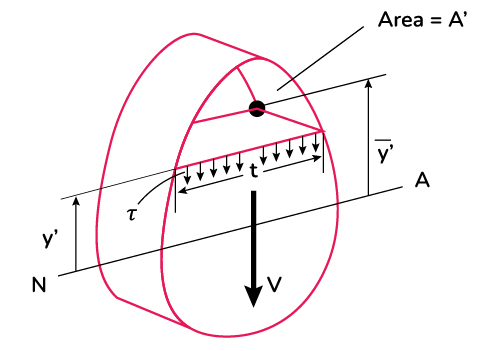
Calculate the shear stress at a distance y' from the neutral axis (NA) of a beam subjected to a shear force V, using the shear formula 𝜏 = VQ/It.
You can use the section modulus calculator (in its advanced mode) to find the neutral axis and moment of inertia of many structural shapes, which will help you to find Q.