Parallel Capacitor Calculator
Our parallel capacitor calculator can quickly obtain the equivalent capacitance for a parallel capacitor circuit.
Ever wondered what happens when you connect two or more capacitors in parallel? In this short text, we will cover everything you need to know to fully understand this subject, including the capacitors in parallel formula.
What is a capacitor?
Before going further on this parallel capacitor calculator, let's start with the basics.
- A capacitor is essentially a device that stores energy in the form of an electric field.
- Capacitors are able to store and release electrical energy, making them useful for a variety of applications, from storing power in our smartphones to regulating voltage in circuits.
This text will focus on what happens when we connect two capacitors in a parallel configuration.
💡 If you want to learn more about capacitors and their working principle, check our capacitor calculator
Capacitors in parallel formula
When capacitors are connected in parallel, their capacitance will simply add together to give you the total capacitance.
Thus, connecting capacitors in parallel allows you to achieve a greater capacitance than you could with a single capacitor since each one will be able to store more energy.
where:
- is the capacitance of the i-th capacitor; and
- is the total or equivalent capacitance of the circuit.
You can input up to ten capacitors in this parallel capacitor calculator. Give it a try!
🔎 Check our capacitors in series calculator to see what happens when we connect the capacitors in series instead!
Why is the equivalent capacitance the sum of all other capacitances?
You may be wondering why the formula is so simple or how it even works (if you read our series resistor calculator, you probably already have an answer).
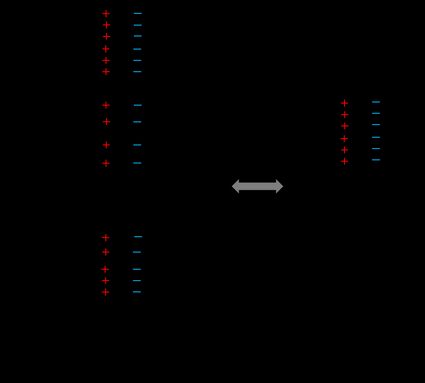
To understand it, let's picture the following scenario, only two capacitors connected in parallel to the same voltage source. We will break it down into a few steps:
- In this situation, the voltage difference across each capacitor is the same.
- If we wanted to find the total charge stored by the capacitors, we would simply add the charge contained in each of them: .
- We can replace this charge with the product of the voltage across the capacitor (which is the same in both of them) and its capacitance: .
- Lastly, we can easily see that dividing by the voltage on each side gives us the capacitors in parallel formula again.
🙋 This equivalent capacitance calculator is straightforward. Just add each capacitance, and it will automatically find the equivalent capacitance for you!