Three-Phase Calculator

The three-phase calculator is a handy tool whenever you need to investigate the three-phase connections, including star and delta type connections. It uses the apparent, active, and reactive powers formulae to solve the problems. Read the following article to learn what three-phase power is and how to use the 3-phase power calculator. Finally, you can also check the three-phase power formulae we're using.

Suppose you're in the middle of apartment or house renovation and looking for helpful tools like the 3-phase power calculator. In that case, you need to check the paint calculator to estimate the paint cost or mortgage calculator to see if it is worth financing the renovation from a loan. Give them a chance!

If you've ever looked at the power lines running to your home or business, you may have noticed that there are usually three wires instead of just one. This is because most power plants generate electricity using three-phase power. Three-phase power is a type of alternating current (AC) electricity where the voltage waves occur at three different times. This provides a more consistent flow of power than single-phase power, which is often used in small businesses and homes.

While three-phase power is more efficient, it can also be more expensive to install and maintain. As a result, it's typically only used in applications where high levels of power are required, such as factories and electric trains.

The three-phase power formula is a mathematical way to calculate the amount of power being used in a three-phase system. This formula takes into account the three different voltages that are present in a three-phase system, as well as the resistance of the load.

To use the three-phase power formula, you'll need to know the voltage of each phase, and the current flowing through the system. Alternatively, you can use the line-to-line voltage and line current. Once you have this information, you can plug it into one of the 3-phase power formulae in the below sections:

1. Apparent power formula
2. Reactive power formula
3. Active power formula

The first equation of a three-phase system we'll look at is the apparent power formula. It has the following form:

where:

• $S$ - The apparent power in VA (volt-amperes); check our kVA calculator to learn more about this unit;

• $V_{\text{Ph}}$ - The phase voltage in V (volts); and

• $I_{\text{Ph}}$ - The phase current in A (amperes).

As you can see in the three-phase calculator, you can also input the line-to-line quantities. In that case, the new apparent power formula is the following:

where:

• $V_{\text{line}}$ - The line-to-line voltage in V; and

• $I_{\text{line}}$ - The line-to-line current in A.

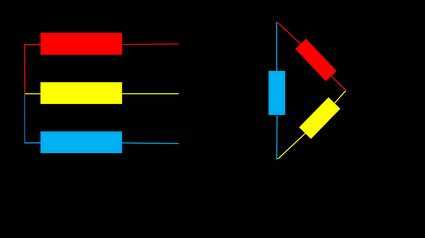
Before we go further, let's discuss the two types of connections (see the picture below) that we have in our three-phase power calculator:

• Star - The 3-phase wires are connected to the common point together with neutral; and
• Delta - The 3-phase wires in the shape of delta Greek letter $\Delta$ with no neutral.

The connection type determines the relationship between phase and line-to-line voltage and current:

• equal currents for star connection and $V_{\text{line}} = \sqrt{3} \cdot V_{\text{Ph}}$; and
• equal voltages for delta connection and $I_{\text{line}} = \sqrt{3} \cdot I_{\text{Ph}}$.

The second three-phase power equation is the reactive power formula. As you probably know, not all of the apparent power is converted into work or heat. Some of it is stored in the capacitors and inductors, which we call reactive power. The reactive power formula has the following form:

where:

• $Q$ - The reactive power in var (volt-amperes reactive);
• $\varphi$ - The phase angle in electrical degrees; and

everything else is the same as in the apparent power formula. You can also use the line values, in which case the three-phase reactive power formula is as follows:

The last three-phase equation we'll discuss is the active power formula. The active power is the amount of power that's actually used to do work:

• $P$ - The active power in W (watts); and

• $\text{PF}$ - The power factor, i.e., the ratio of real power to the apparent power (varies between -1 and 1).

As before, you can also use the line values to calculate the three-phase active power. In that case, the three-phase watts formula is as follows:

Now that you know the three-phase power equations and what 3-phase power is, let's see how to use our 3-phase current calculator:

1. First, select the type of connection (star or delta).
2. Then, input the values for voltage, current, and phase or power factor.
3. The three-phase power calculator will automatically calculate the apparent power, reactive power, and active power.

If you're working with a three-phase system, you may need to convert the power from watts to kilowatts. This can be done by simply dividing the power in watts by 1,000.

For example, if the three-phase power is 10,000 watts, the three-phase power in kilowatts would be 10 kilowatts. Our 3-phase calculator has a built-in unit switcher, making the 3-phase conversion very easy.