Archimedes' Principle Calculator

With this Archimedes' principle calculator, you can measure the density of a crown or study the changes in mass and weight of a submerged object in a fluid or the buoyant force. In any case, we have you covered!

When King Heiron II of Syracuse was unsure if the goldsmith made him a crown of pure gold or not, he requested Archimedes to figure it out. While taking a bath, Archimedes noticed that as he submerged in the water, the water level raised, and Eureka! All he had to do was to immerse the crown in water to obtain its mass in water, compare it to its mass in air, and with the displaced volume of water, determine the crown's density 👑

Keep reading to learn:

• What the Archimedes' principle is;
• The Archimedes principle formula, or buoyant force equation; and
• The law of floatation.

Let's sink in!

If you've ever gone swimming at the beach or pool, you might have noticed that objects feel lighter in water than in air. Have you ever wondered why this happens? Well, the answer was found by the Greek physicist Archimedes around the year 246 BC and is summarized in a principle named after him.

Archimedes' principle states that when a body is partially or completely submerged in a fluid, it's subjected to an upward force equal to the weight of the displaced fluid.

This upward force, also known as the buoyant force or buoyancy, opposes the object's weight, resulting in an apparent lighter object. The denser the liquid the object is immersed in, the greater the magnitude of the upward force.

Because the density of water $(\rho_{\text{water}} = 1000 \text{ kg/m}^3)$ is greater than the one for air $(\rho_{\text{air}} = 1.275 \text{ kg/m}^3)$, the upward force associated to water is higher and the apparent weight of the object will be significantly lower when submerged in water compared to air.

This will become clearer in the next section, where we introduce Archimedes' principle formula or buoyant force equation.

Now that we've seen what Archimedes' principle is about, we can introduce the related formula. This is the equation to calculate buoyancy force or Archimedes' principle formula:

where:

• $F_B$ – Buoyant or upward force;
• $\rho$ – Density of the fluid;
• $g$ – Acceleration due to gravity; and
• $V$ – Volume of fluid displaced by the object.

Earlier we mentioned that the apparent weight of an object is lower in water $(\rho_{\text{water}} = 1000 \text{ kg/m}^3)$ that in air $(\rho_{\text{air}} = 1.275 \text{ kg/m}^3)$. Because the buoyancy force is directly proportional to the density of the fluid, the higher the density, the greater the buoyant force.

Note that if we multiply the fluid's density by the volume of displaced fluid by the object, we get the mass of the fluid $m_{\text{fluid}}$. Thus, we can also express the buoyant force as the weight of the displaced fluid $W_{\text{fluid}}$:

You can learn more about volume and mass relationship with our volume to mass calculator

As you can see in the figure below, when an object is submerged in a fluid, the fluid exerts two vertical forces, one on the top, $F_1$, and the other on the bottom, $F_2$.

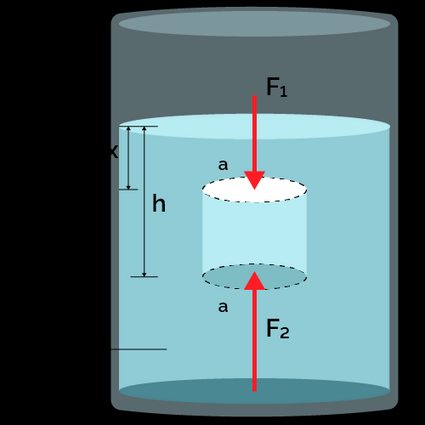
Because pressure increases with depth, the bottom force is always higher than the top one $(F_2 > F_1)$. This means that the resultant force between them will always be an upward force, known as the buoyant force $F_B$:

If you're unsure why pressure increase with depth, check our hydrostatic pressure calculator to find out!

The law of floatation, or principle of floatation, indicates that any floating object displaces its own weight of fluid.

The above indicates that for a body to float on a fluid, the buoyant force $F_B$ must be greater than the object's weight $W_{\text{obj}}$, else the object will sink in the fluid.

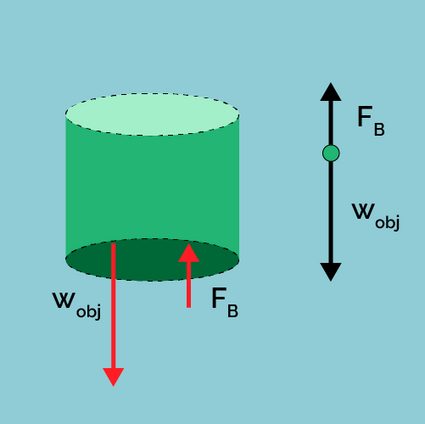
• If $F_B > W_{\text{obj}}$ – Object floats;
• If $F_B = W_{\text{obj}}$ – Object is in neutral equilibrium, that is, it remains in place without either rising or sinking; and
• If $F_B < W_{\text{obj}}$ – Object sinks.

You can learn more about buoyancy with our buoyancy calculator!

This Archimedes principle calculator is a versatile tool that you can use to calculate the buoyancy force or the density of an object. Let's see how to use this tool!

To find the buoyant force

This is how to use this tool to find the buoyant force:

1. In the Properties of the object section, indicate the values for True mass of the object and Density of the object.
2. Select the fluid from the drop-down menu at the Properties of the fluid section. For custom fluids, input the density in the Density of the fluid field.
3. Once all these are defined, the calculator will show you the result for the Force of buoyancy.

To find the density of an object

To determine the density of an unknown object, follow these steps:

1. Enter the True mass of the object and the Apparent mass of the object in the Properties of the object section.
2. Using the drop-down menu, choose Fluid type as water. The density field will auto-populate.
3. The Archimedes' principle calculator will display the Density of the object in the Properties of the object section.