Hydraulic Radius Calculator
This is our hydraulic radius calculator, a simple yet powerful tool that we'll help you calculate the hydraulic radius and wetted perimeter of pipes and channels. How? Simply select the type of conduit you're interested in, input some values, and the calculator will have your results in a snap!
If you're a fluid mechanics enthusiast or want to learn more about this topic, we recommend you look at the article we've created. This is what you can expect:
-
What the hydraulic radius is;
-
The hydraulic radius formula;
-
How to calculate the hydraulic radius of a circular pipe and channels; and
-
How to find the wetted perimeter of a circle and other shapes.
What is the hydraulic radius?
The hydraulic radius is a very commonly used parameter in the calculations for open channels and pipes, particularly non-circular pipes. In general terms, the hydraulic radius is defined as the ratio between the cross-sectional area and the wetted perimeter of the channel or conduit:
where:
- — Hydraulic radius, in units of length;
- — Cross-sectional area of pipe or channel; and
- — Wetted perimeter.
Along with the hydraulic radius, we have the hydraulic diameter. This one is not equivalent to twice the hydraulic radius, but rather:
In open channels, the hydraulic radius is an indicator of the channel's efficiency, or its capacity to move water and sediments. Manning's equation, which we use to estimate flow velocity in open channels, includes the hydraulic radius.
The hydraulic radius (or hydraulic diameter) is also used to calculate Reynold's number in circular and non-circular pipes to determine whether a flow is laminar or turbulent, or in the Darcy-Weisbach equation, to find the head loss associated with friction in a pipe.
Hydraulic radius equations
As you can see, the hydraulic radius definition is quite general, and depending on the particular cross-sectional shape you're working with, more specific expressions can be derived. Let's see, for example, how to calculate the hydraulic radius of a pipe of radius .
To keep things simple, we'll look at the case of a full pipe. From the general hydraulic radius equation, we can see that all we need to do is substitute the cross-sectional area and the wetted perimeter :
In the case of a full pipe, and (we'll talk about wetted perimeter in the next section 😉). By substituting these:
This corresponds to the hydraulic radius of a pipe. All that is left is to insert the particular radius value you're working with.
By following these same steps, you can derive an expression for the hydraulic radius of a trapezoidal channel or any other conduit. In the table below, we have included the hydraulic radius equation for this geometry and other configurations such as partially filled circular pipes and common channels shapes:
Shape | Hydraulic radius equation | |
|---|---|---|
Pipe (full) |
|  |
Pipe (less than half-full) |
|  |
Rectangular channel |
|  |
Trapezoidal channel |
| 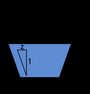 |
Triangular channel |
| 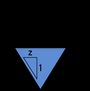 |
These are the equations we've included in this hydraulic radius calculator! This way, you can simply substitute your values, and we'll handle the heavy lifting for you 😎
How to find the wetted perimeter
In open channels and pipes, the wetted perimeter corresponds to the total surface that's in contact with the flowing liquid. As you may expect, the higher the wetted perimeter, the greater the friction losses, and hence the larger the head drop.
The general formula to find the wetted perimeter is comprised of the sum of the lengths of all the surfaces that are in contact with the fluid:
where:
- — Wetted perimeter of the channel or pipe, in length units;
- — Number of surfaces in contact with the fluid; and
- — Length of side .
From this equation, we can obtain the formula for any particular shape. Below we've included some of the formulas for commonly used shapes:
Shape | Wetted perimeter formula | |
|---|---|---|
Pipe (full) |
|  |
Pipe (less than half-full) |
|  |
| ||
Rectangular channel |
|  |
Trapezoidal channel |
|  |
Triangular channel |
|  |