Time of Flight Calculator - Projectile Motion

If you're interested in how to find how long something is in the air, this time of flight calculator is what you need. This tool finds the time of flight in projectile motion as long as you know the initial velocity, angle of launch, and initial height.

Keep reading to know the time of flight equation and better understand the theory behind this calculator.

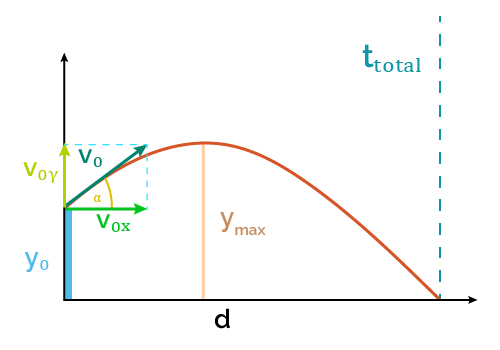
Time of flight is the time that occurs from the projectile launching to when it hits the ground. In other words, it is the amount of time it remains in the air.

To calculate the time of flight, input the following values in the calculator:

1. Velocity: refers to the speed of launch of the projectile. If you click in the advanced mode, you can input its horizontal and vertical components instead.

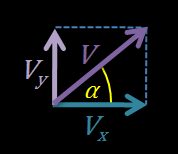
2. Angle of launch: it is the angle formed between the velocity vector and the ground (or between the velocity vector and its horizontal component). When this angle equals zero (α = 0), the motion is called horizontal projectile motion.
3. Initial height: Sometimes, the projectile is not launched from the ground but from another surface above it. A higher initial height implies more time of flight in the projectile motion. In case the projectile launching doesn't occur from above the ground, just input zero as the initial height.

The formula for the time of flight of a projectile is:

where:

• $t_\text{total}$ — Time of flight, calculated in seconds (s);
• $V_{0y}$ — Initial vertical velocity, in meters per second (m/s);
• $\text{g}$ — Gravity acceleration, in meters per square second (9.807 m/s²);
• $y_0$ — Initial height, in meters (m).

If we don't know the vertical component of the initial velocity (V_0y), we can calculate it using the total initial velocity (V₀) and the angle of launch (α):

Therefore, another version of the time of flight equation is:

As an example, for an initial velocity of 20 m/s, an 30 degrees angle of launch, and an initial 2 m height, the calculation would be:

And that's it for now! Thanks for reading up here. Hopefully, now you possess a better understanding of what's behind this calculator.