Combination Calculator
This combination calculator, or nCr calculator, helps you calculate the number of combinations or permutations in a set (often denoted as nCr) and generates the list of every single possible combination or permutation (up to the length of 20 elements).
If you switch on the advanced mode of this combination calculator, you'll find the number of permutations.
If you still have doubts about the difference between permutation and combination, we'll explain it in the following article. You'll find the difference between those two terms and the nCr formula.
Combinations and permutations have many applications:
- Have you wondered about your chances of winning the main prize in a lottery? How probable is winning the second prize? To answer both and other similar questions, you need to use combinations. Speaking of money, have you already seen the Harry Potter currency calculator, which shows how wizards paid in this Universum? It's worth checking for sure!
- Physicists use permutation to predict theoretical material properties relevant to everyday life, such as the average velocity of gas particles, which is strongly related to the of those particles and, consequently, their temperature and .
Difference between combination and permutation calculation
When studying statistics, we usually confuse combinations and permutations. Before using this calculator, we must know the difference.
- Combination: Calculates the number of ways you can choose r elements out of a set containing n distinct objects, no matter the order. There are two types of combinations:
- Combinations with repetition.
- Combinations without repetition.
- Permutation: Like combinations, it calculates the number of ways you can choose r elements out of a set containing n distinct objects but taking all the possible orders into account. Each possible ordering of the same group of elements accounts for an additional permutation. Similarly, there are two types of permutations:
- Permutations with repetition.
- Permutations without repetition.
As these definitions can be a bit confusing and a picture worth a thousand words, we created the following graphic, which describes perfectly these concepts and their differences.
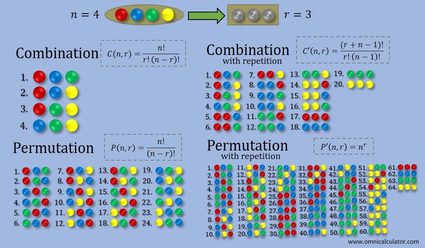
nCr formulas to calculate combinations and permutations
The following table contains the formulas to calculate the number of combinations and permutations. The exclamation mark stands for the factorial, which you can calculate with our exclamation point calculator, or simply, factorial calculator.
Arrangement type | Formula | |
|---|---|---|
Combination | Without repetition |
|
With repetition |
| |
Permutation | Without repetition |
|
With repetition |
| |
In the previous formulas:
- — Number of possible combinations without repetition;
- — Number of possible combinations with repetition;
- — Number of possible permutations without repetition;
- — Number of possible permutations with repetition;
- — Total number of objects;
- — Sample size.