Area of a Rectangle Calculator

With the rectangle area calculator, you can find the area (and almost any parameter) of a rectangle.

This rectangle area calculator doesn't just calculate the area. It can also:

• Find the dimensions of any rectangle given its area or perimeter;
• Calculate the perimeter of any rectangle; and
• Find the diagonal of any rectangle.

This is a complete rectangle calculator! Read the short article below to know more about rectangles and how to calculate the area of a rectangle.

A rectangle is a four-sided irregular polygon with four right internal angles. Every rectangle's side is equal in length to the one directly in front. Also, its adjacent sides must be different (otherwise, it would be a square).

This simple definition encloses some mathematical relations between a rectangle's parameters. Let's look at some of its formulas.

Finding the area of a rectangle is really simple. All you need to do is multiply its length and width dimensions together:

where:

• $a$ is the rectangle's length;
• $b$ is the rectangle's width; and
• $A$ is the resulting area of the rectangle.

To calculate the perimeter of a rectangle, we need to add the length of each of its sides.

Alternatively, since we know that opposite sides are equal in length, all we need is the length of two of them.

Therefore, from its length and width, we get:

where:

• $a$ is the rectangle's length;
• $b$ is the rectangle's width; and
• $P$ is the rectangle's perimeter.

Finding the diagonal of a rectangle is the same as using the Pythagorean theorem.

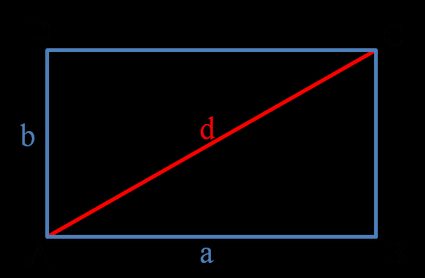
Using the diagonal as the hypotenuse and the rectangle's width and length as a triangle's sides:

where again:

• $a$ is the rectangle's length;
• $b$ is the rectangle's width; and
• $d$ is the rectangle's diagonal.

Finally, let's say you want to find the rectangle's dimensions given its area or perimeter.

We can rearrange the equations to get different expressions for each dimension.

Width:

• $b = A/a$;
• $b = P/2 - a$; and
• $b= \sqrt{d^{2} - a^{2}}$

Length:

• $a = A/b$
• $a = P/2 - b$;
• $a= \sqrt{d^{2} - b^{2}}$

where:

• $a$ is the rectangle's length;
• $b$ is the rectangle's width;
• $d$ is the rectangle's diagonal;
• $P$ is the rectangle's perimeter; and
• $A$ is the rectangle's area.