Regular Polygon Calculator
Welcome to the regular polygon calculator, where you'll be able to:
- Calculate the area of regular polygons;
- Calculate the perimeter of those polygons; and
- Calculate other regular polygon features, such as radius and angles.
With this tool, you can calculate regular octagons, hexagons, triangles, and many other shapes. For example:
- To calculate a regular triangle, input 3 as the number of sides.
- To calculate a regular hexagon, in the calculator, input 6 as the number of sides.
- To calculate a regular octagon, input 8 as the number of sides.
In the nomenclature section, you can see the number of sides corresponding to each regular polygon name.
🙋 This tool calculates the area only of regular triangles. If you want to calculate the area of any kind of rectangle, you use our triangle area calculator. The same applies to 4 - sided polygons (rectangles), whose area you can calculate with our rectangle area calculator.
What is a regular polygon - Definition
A regular polygon is only one of the sons of the polygon family. A polygon is a 2D closed figure made up of straight-line segments. Based on their sides and angles, we can classify polygons differently.
A regular polygon is a polygon that has the following characteristics:
- Equiangularity - in an equiangular polygon, all angles are equal in measure.
- Equilaterality - in an equilateral polygon, all sides have the same length.
Depending on the number of sides, the polygon will have a different name and form different angles.
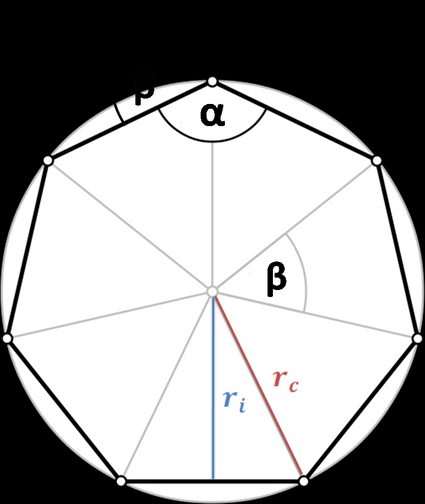
The angles that distinguish a polygon are:
- Interior angle (α): The angle formed by any two adjacent sides.
- Exterior angle (β): The angle formed by two adjacent vertices and the polygon center.
Additionally, we can define other two characteristics of these polygons:
- Aphothem (ri): Also known as incircle radius, it is the line segment from the polygon center to the midpoint of any polygon side.
- Circumradius (rc): The radius of the circle that passes through all the vertices of the polygon.
Now that you know what a regular polygon is let's see how to name them as a function of the number of sides.
Regular polygon nomenclature
The following table shows the names of regular polygons and their angles according to the polygon's number of sides (n).
n | Name | Shape | α | β |
|---|---|---|---|---|
3 | Triangle | π/3 = 60° | 2π/3 = 120° | |
4 | Square | π/2 = 90° | π/2 = 90° | |
5 | 3π/5 = 108° | 2π/5 = 72° | ||
6 | Hexagon | 2π/3 = 120° | π/3 = 60° | |
7 | Heptagon | 5π/7 = 128.57° | 2π/7 = 51.43° | |
8 | Octagon | 3π/4 = 135° | π/4 = 45° | |
9 | Nonagon | 7π/9 = 140° | 2π/9 = 40° | |
10 | Decagon | 8π/10 = 144° | π/5 = 36° | |
n | n - gon | 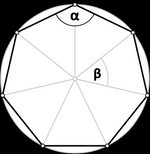 | (n-2) × 180°/n | 360°/n |
Regular polygon formulas for area, perimeter, angles, and radius
To calculate any regular polygon area, perimeter, or radius, we only need to know the number of sides (polygon shape) and its side length. To calculate the angles, only the number of sides is necessary.
-
Area formula for a regular polygon
area = n × a² × cot(π/n) / 4where:
n— number of sides; anda— side length.
If you have doubts about the units of area, look at our area converter.
-
Perimeter
perimeter = n × a

-
Interior (α) and exterior (β) angles :
α = (n - 2) × π/n;β = 2 × π/n
-
Incircle radius (apothem)
rᵢ = a/[2 × tan(π/n)] -
Circumcircle radius
r꜀ = a/[2 × sin(π/n)]
Our regular polygon calculator uses all those equations. With these formulas, you can calculate regular triangles, squares, and many more shapes.