Mass Moment of Inertia Calculator
This mass moment of inertia calculator will help you determine the mass moment of inertia of any common figures like spheres, rectangular prisms, cylindrical objects, and more.
Keep on reading to learn about:
- What moment of inertia is;
- How to calculate moment of inertia;
- The mass moment of inertia equation;
- The mass moment of inertia table; and
- How to use this mass moment of inertia calculator.
What is moment of inertia?
Mass moment of inertia is the amount of torque or moment needed to make an object rotate or experience an angular acceleration about an axis.
An object's mass moment of inertia gives us an idea of how much rotational inertia the object can have with respect to an arbitrary rotational axis. The larger the moment of inertia of an object is, the harder it is to gain rotational kinetic energy or the harder it is to stop from turning.
To know what the moment of inertia of an object is, take the product of the torque needed to rotate that object and the applied torque's distance from the axis of rotation. However, there is a much better and correct way of doing it, and we'll discuss that in the next section of this text.
The mass moment of inertia equation and table
To calculate the mass moment of inertia, , let us consider a point of material with mass, , which is at a distance from an arbitrary axis of rotation, which we denote as .
We can calculate its mass moment of inertia by taking the product of its mass by the square of its distance from its axis of rotation, as shown in the equation below:
To determine an object's mass moment of inertia, we can consider all its points' mass moment of inertia, and sum them all up. We can express that in equation form shown below:
Where:
- is the total number of material points in an object;
- is the representation of each point in the object and has values from to ;
- is the summation symbol for sample ;
- is the mass of material point; and
- is the distance of material point from the axis of rotation.
We can also divide our object into very tiny points with equal masses and use calculus to find an object's mass moment of inertia. We can do that by evaluating the integral over these set point masses, as expressed in the moment of inertia formula below:
Moment of inertia table
We can then use the moment of inertia formula integration to derive other formulas for objects that come in specific shapes like cube, cylinder, sphere, and so on, as shown in the mass moment of inertia table below:
No. | Figure and moments of inertia |
|---|---|
#1 - Ball. Solid ball of radius r and mass m with axis of rotation going through its center. | 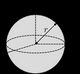 |
 | |
#2 - Circular hoop. Thin circular hoop of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. |  |
 | |
 | |
#3 - Cuboid. Solid cuboid of length l, width w, height h and mass m with four axes of rotation going through its center: parallel to the length l, width w, height h or to the longest diagonal d. |  |
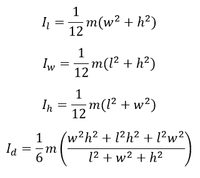 | |
#4 - Cylinder. Solid cylinder of radius r, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes. |  |
 | |
 | |
#5 - Cylindrical tube. Cylindrical tube of inner radius r₁, outer radius r₂, height h and mass m with three axes of rotation going through its center: parallel to x, y and z axes. |  |
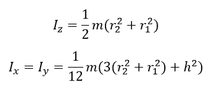 | |
#6 - Cylindrical shell. Cylindrical shell of radius r and mass m with axis of rotation going through its center, parallel to the height. | 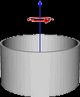 |
 | |
#7 - Disk. Thin solid disk of radius r and mass m with three axes of rotation going through its center: parallel to the x, y or z axes. | 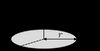 |
 | |
 | |
#8 - Dodecahedron. Solid and hollow, regular dodecahedron (twelve flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. |  |
 | |
 | |
where: | |
 | |
#9 - Ellipsoid. Solid ellipsoid of semiaxes a, b, c and mass m with three axes of rotation going through its center: parallel to the a, b or c semiaxes. |  |
 | |
 | |
 | |
#10 - Icosahedron. Solid and hollow, regular icosahedron (twenty flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. |  |
 | |
 | |
where: | |
 | |
#11 - Isosceles triangle. An isosceles triangle of mass m, vertex angle 2β and common-side length L with axis of rotation through tip, perpendicular to plane. | 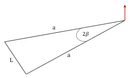 |
 | |
#12 - Octahedron. Solid and hollow, regular octahedron (eight flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. | 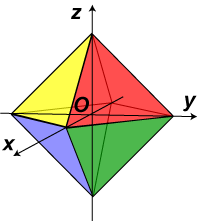 |
 | |
 | |
#13 - Point mass. Point mass m at a distance r from the axis of rotation. | 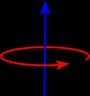 |
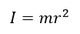 | |
#14 - Rectangular plate. Thin rectangular plate of length l, width w and mass m with axis of rotation going through its center, perpendicular to the plane. |  |
 | |
#15 - Regular polygon. Plane regular polygon with n vertices, radius of the circumscribed circle R and mass m with axis of rotation passing through its center, perpendicular to the plane. Radius R can be expressed with side s. |  |
 | |
 | |
#16 - Right circular cone (hollow). Hollow right circular cone of radius r, height h and mass m with three axes of rotation passing trough its center: parallel to the x, y or z axes. |  |
 | |
 | |
#17 - Right circular cone (solid). Solid right circular cone of radius r, height h and mass m with three axes of rotation passing trough its center: parallel to the x, y or z axes. | 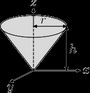 |
 | |
 | |
#18 - Rod. Rod of length L and mass m with two axes of rotation: about its center and one end. | 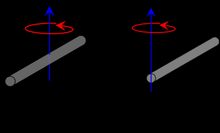 |
#19 - Sphere. Hollow sphere of radius r and mass m with axis of rotation going through its center. |  |
 | |
#20 - Spherical shell. Spherical shell of inner radius r₁, outer radius r₂ and mass m with axis of rotation going through its center. |  |
 | |
#21 - Tetrahedron. Solid and hollow, regular tetrahedron (four flat faces) of side s and mass m with axis of rotation going through its center and one of vertices. | 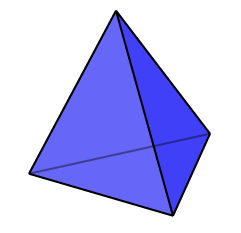 |
 | |
 | |
#22 - Torus. Torus with minor radius a, major radius b and mass m with axes of rotating going through its center: perpendicular to the major diameter and parallel to the major diameter. | 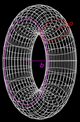 |
 | |
#23 - Two point masses. Two point masses m₁ and m₂, with reduced mass μ, separated by a distance r with axis of rotation going through the center of mass and perpendicular to the line joining the two particles. |  |
 |
It's also worth noting that we use , , or as mass moment of inertia units. You can use that as a distinction against the second moment of area units, which are in the forms of or . You can learn more about the second moment of area by checking out our separate moment of inertia calculator.
How to use this mass moment of inertia calculator
Here are the steps you can follow when using our mass moment of inertia calculator:
- Select the figure that matches the object's shape that you want to find the mass moment of inertia. You can choose from more than 20 figures in our tool.
- Enter the mass of your object.
- Input the distance measurement that our calculator requires you to enter. This distance depends on the figure you selected. Our mass moment of inertia calculator will use this measurement to determine the moment arm or the distance, , suitable for your object of choice.
And that's it! Our mass moment of inertia will already display the mass moment of inertia about an axis (or various axes), depending on the figure you choose. You can also change the moment of inertia units by clicking on the dropdown arrow beside the calculated value.