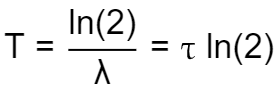Half-Life Calculator

Whether you are considering radioactive atoms or a population of bacteria, the underlying mathematics is the same: our half-life calculator will teach you how to compute the most important quantity of the decay process, the half-life.

Here you will learn:

• What is the half-life in exponential decays;
• How to calculate the exponential decay using the half-life;
• How to calculate the half-life;
• Examples of half-life in physics and biology.

A decay process is any process that sees a decrease in the measured quantity. Decay processes are usually divided into two categories:

• Exponential decays; and
• Non-exponential decays, where we can identify subtypes like:
  • Inverse square decay; or
  • Zipf's law decay

In any decay process, we can pinpoint a moment in which the quantity is half the original amount. We call the time elapsed from the starting moment to this point the half-life of the quantity.

We can define the half-life also in terms of probability. This approach best suits discrete quantities or unitary ones. In this case, the half-life is the time after which there is a $50\%$ chance of decay.

In physics, the half-life usually describes stochastic processes as radioactive decay, where an unstable atom emits or absorbs a particle to change species. This process is entirely random, and an atom can go eons without decaying. On the contrary, in biology, a bacteria in a decaying population will die after a given time: no immortal bacteria out there.

Let's learn how to calculate the half-life of an exponential decay (a mathematical model based on the exponential growth).

We define first the law of exponential decay:

Where:

• $N(t)$ is the quantity at the time $t$;
• $N(0)$ is the quantity at the initial reference time;
• $t$ is the elapsed time; and
• $\tau$ is the average lifetime of each component of the measured quantity.

To find the half-life we can rearrange this expression, knowing that, when the half-life time is reached:

We can define the half-life time $t_{0.5}$ as:

Which can be easily rewritten to isolate $t_{0.5}$ using the natural logarithm:

Using this relation, we can write the half-life equation using the factor $0.5$ characteristic for the halving of the quantity:

Our half-life calculator works in both directions: you can calculate the half-life of a decay process if you know the initial and final quantities, and the elapsed time, or you can calculate the final (or initial) quantities if you know the half-life.

We will calculate the half-life in two situations: radioactive decay and the decline of a bacterial population.

Take a radioactive atom, let's say promethium (were you expecting uranium?). Promethium is the lightest natural radioactive element. Its most common (and stable) isotope, $^{145}\text{Pm}$, has half-life $t_{0.5}=17.7\ \text{y}$. Scientists estimate that on Earth, there are about $500\ \text{g}$ of promethium at a given time. Assuming that no more atoms of this element would form, how much promethium would we have after $100\ \text{y}$? Input the known data in the half-life equation:

Let's try the other way around. What's the half-life of a bacteria population that starts with $10^5$ individuals, and after a day ends with $5\cdot 10^3$ individuals. Input the data in our half-time calculator:

Now, if you knew the energy released after $52 \ \mathrm{min}$, you could calculate the power to estimate how many watts such a decay generates. Then, Omni Calculator's power converter might be the next step to express power in more adequate units. That would be very interesting to check!