Thermal Resistance Calculator

Calculating the thermal resistance is one of the fastest ways to relate an object's temperature drop to its heat transfer rate. With this tool, you can calculate the thermal resistance of the three most common shapes: a plate, a hollow cylinder, and a hollow sphere. For example, you can use it to calculate the thermal resistance of a copper member, as long as you input its dimensions.

Don't you know how to calculate thermal resistance from thermal conductivity? In the following sections, we present the thermal resistance equations for the three shapes of the calculator.

In thermal engineering, thermal resistance appears as a tool to relate the temperature difference to the heat transfer rate.

For example, we know that the magnitude of the heat conduction rate through a plate is given by:

, where:

• $\dot Q$ — Heat transfer rate magnitude, in watts (W) or BTU per hour (BTU/h);
• $t$ — Plate thickness, in meters (m) or feet (ft);
• $A$ — Plate area, in m² or ft²;
• $\Delta T$ — Difference between the left and right sides temperatures ($T_1$ and $T_2$, respectively), in degree Celsius (°C) or Fahrenheit (°F); and
• $k$ — Thermal conductivity, in W/(m K) or BTU/(h ft °F).

We can express the previous equation the following way:

where $R_\text{plate}$ is the thermal resistance of the plate, in kelvins per watt (K/W), and is equal to:

As its name suggests, thermal resistance indicates how averse a system is to the flow of heat through it. The higher it is, the lower the heat transfer rate for the same temperature difference.

Note that this relationship is analogous to Ohm's law:

For the specific case of conduction through a plate, $R_\text{plate}$ is also analogous to the wire resistance formula.

In the previous section, we discussed the meaning behind thermal resistance using heat flow through a plate. We can do something similar for a hollow cylinder and sphere and obtain formulas for their thermal resistance.

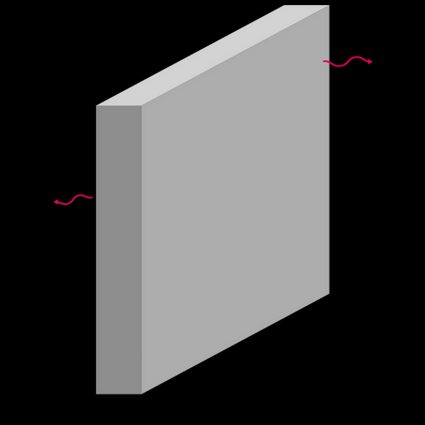
• Thermal resistance equation for a plate:

  $R_\text{plate} = \frac{t}{kA}$

  • $t$ — Plate thickness, in meters (m) or feet (ft);
  • $k$ — Thermal conductivity, in W/(m K) or BTU/(h ft °F).
  • $A$ — Plate area (i.e., $A=l \times w$), in m² or ft²;

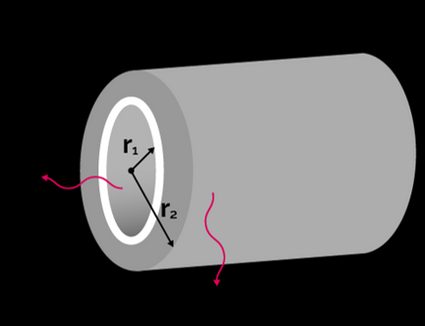
• Thermal resistance equation for a hollow cylinder:

  $R_{\text{cylinder}} = \frac{\ln(r_2/r_1)}{2\pi Lk}$

  • $r_1$ and $r_2$ – Internal and external cylinder radius, in meters (m) or feet (ft);
  • $L$ — Length of the cylinder, in meters (m) or feet (ft);

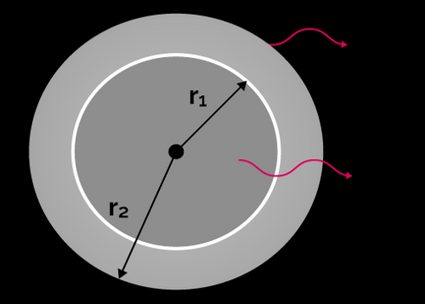
• Thermal resistance equation for a hollow sphere:

  $R_{\text{sphere}} = \frac{r_2-r_1}{4\pi r_1r_2k}$

  • $r_1$ and $r_2$ – Internal and external sphere radius, in meters (m) or feet (ft);