Buckling Calculator

This buckling calculator estimates the critical load of a column, which is the compressive force that will cause the column to suffer buckling and collapse before even reaching the yield stress.

To obtain the critical buckling load, input the effective length factor (or the boundary condition), the radius of gyration (or moment of inertia and area), and the column length (or effective length). The calculator will use the critical buckling load formula and give you the answer.

Keep reading this article to learn the Johnson and Euler buckling formulas for columns, which are the ones used by this calculator.

The formula to calculate the critical load will depend if the column is "long" or "short." We select the appropriate equation in the buckling calculator. A short column is less likely to fail due to buckling and more prone to fail by compression than a long column.

But what do we mean by a short or long column? The answer is in the slenderness ratio ($S$) and the critical slenderness ratio ($S_\text{cr}$), properties of the column:

, where:

• $L_\text e = LK$ — Effective length, the product of the column length ($L$) and effective length factor ($K$);
• $R = \sqrt{I/A}$ — Radius of gyration, a function of the column moment of inertia ($I$) and the cross-sectional area ($A$);
• $E$ — Young's modulus of the column material; and
• $\sigma_\text Y$ — Yield strength of the column material.

The following are some important aspects of the previous equations:

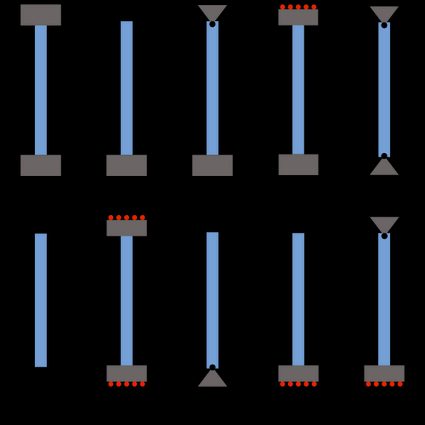
• The effective length factor $K$ (image below) depends on the boundary conditions applied to the column. You can look at it in this critical load calculator by switching between different boundary conditions.
• The moment of inertia to choose will be the lower one between the two axes ($I = \min(I_x,\ I_y)$. You can obtain it with our moment of inertia calculator.
• As you can note, the slenderness ratio ($S$) is a geometrical property, while the critical slenderness ratio ($S_\text{cr}$) is a material property.
• Once we know $S$ and $S_\text{cr}$, we can use the appropriate buckling equation that is included in the buckling calculator.

In the previous section, we presented the formulas for obtaining the slenderness ratio ($S$) and the critical slenderness ratio ($S_\text{cr}$). Once we know those values, we're ready to use the appropriate column buckling formula and calculate the critical load.

If $S > S_\text{cr}$, the column is "long," and we use the Euler buckling formula:

If $S < S_\text{cr}$, the column is "short," and we use the Johnson's formula:

If you didn't look at it, switch back to the previous section of this buckling calculator, where we explain the different terms used in the buckling equations above ($E$, $I$, $L$, $L_\text e$, $\sigma_\text Y$, $A$, $R$).