Young's Modulus Calculator

With this Young's modulus calculator, you can expect to quickly determine an object's modulus of elasticity. Whether you have the values for applied axial force and changes in length or the stress and strain points from a tensile test, this tool will calculate Young's modulus associated.

Keep reading to learn:

• What Young's modulus is;
• The linear relationship between stress and strain;
• How to calculate the modulus of elasticity from a stress-strain curve; and
• How to calculate Young's modulus with the modulus of elasticity formula.

One of the main goals when designing structures is to guarantee they are safe for their intended purpose. This signifies that we want designs that can withstand a given load while keeping deformations as small as possible.

An important factor that we consider in the design and analysis of structures is a material's property known as Young's modulus or modulus of elasticity, denoted by the letter $E$.

The modulus of elasticity represents how difficult or easy it's to deform a material when an axial load is applied. The greater the value of $E$, the fewer deformations it'll experience. For example, steel has a modulus of elasticity of 200 GPa and wood of approximately 2 GPa. This means that for the same load, a rod made of wood will show higher deformations than the same geometry rod made of steel.

Even though in everyday life, we wouldn't (and shouldn't) see a bridge bending or a beam deflecting, the truth is that they do deflect, but in such a little amount that we can't perceive it at bare sight. Deflections are considered during the design of a structure to ensure that when they occur, they do within the material's elastic range.

When we apply an axial load, the material will extend or compress. If the material recovers its initial geometry when we remove the load, exhibiting no deformations, we call this the material's elastic range. Loads beyond this elastic range will result in permanently deformed or fractured objects.

This is exactly the behavior we observe in a graphic known as the stress-strain curve, as shown in the image below. The data plotted in these types of curves comes from an empirical test known as the tensile test, from which it's possible to calculate the applied stress $(\sigma)$ plotted on the y-axis and the deformations or strain $(\varepsilon)$ on the x-axis.

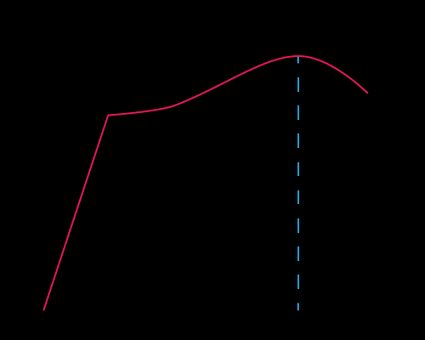
Note that the first part of the plot is a straight line (up to the black dashed line); this represents the material's elastic range. Just like any other linear relation between variables, we can use the equation of a line to describe the relationship between stress and strain:

In our case, $x = \text{Strain}$, $y = \text{Stress}$, and $c= 0$ (intersection at origin):

In this case, the slope $m$ corresponds to the modulus of elasticity of the material, then:

or

where:

• $\sigma$ – Stress;
• $E$ – Young's modulus or modulus of elasticity; and
• $\varepsilon$ – Strain.

Note this expression is similar to Hooke's law formula for a spring, $F =-k \cdot x$. In fact, the linear stress equation is a particular case of Hooke's, with E representing the proportionality factor.

With this Young's modulus calculator, you can plot up to ten points, from which the calculator will determine the material's linear range and the modulus of elasticity $E$. For this:

1. Select the Stress-strain curve option from the calculator's drop-down menu.

2. Then, proceed to enter the values for at least three pairs of stress-strain points $(\varepsilon, \sigma)$.

3. The calculator will plot your curve and indicate Young's modulus value.

We can rearrange the linear stress equation from above to get an expression for Young's modulus $E$. This is Young's modulus formula:

where:

• $\sigma$ – Stress;
• $E$ – Young's modulus or modulus of elasticity; and
• $\varepsilon$ – Strain.

To calculate the stress $\sigma$, you can do so by relating the applied load and the cross-sectional area of the object:

where:

• $\sigma$ – Stress;
• $F$ – Axial load; and
• $A$ – Cross-sectional area.

You may find more about stress with the stress calculator!

To determine the strain $\varepsilon$ in terms of the changes in the length of the object:

where:

• $\varepsilon$ – Strain;
• $L$ – Final length; and
• $L_0$ – Initial length.

Once you've calculated the stress and strain, substitute them in Young's modulus formula to calculate the elastic modulus.

Since the strain is unitless, the modulus of elasticity will have the same units as the tensile stress (psi or Pa).

The Young's modulus calculator also offers you this methodology for calculating the elastic modulus of a material! Let's see how to calculate Young's modulus with this tool:

1. Select the Single stress/strain value option from the' Calculate from' field.

2. In the Stress section, input the numbers for Force (F) and Area (A); the calculator will determine the Stress (σ).

3. Similarly, in the Strain section, fill in the rows corresponding to Final length (L) and Initial length (L₀); the calculator will show the value for the Strain (ε).

4. Finally, once all these values are determined, the calculator will display the Young's modulus (E) in the Result section.