Car Center of Mass Calculator

Welcome to the car center of mass calculator! With this tool, you can calculate the center of gravity of a race car, sedan, or any type of vehicle. Calculating the center of balance or center of mass of a car is essential to study its stability and performance.

Keep reading to learn:

• What the center of mass is;
• The general center of mass formula; and
• How to calculate a car's center of gravity using this car center of mass calculator.

Or you can check the car crash calculator to find out the g-force that acts on passengers during a car crash.

Let's go! 🚗

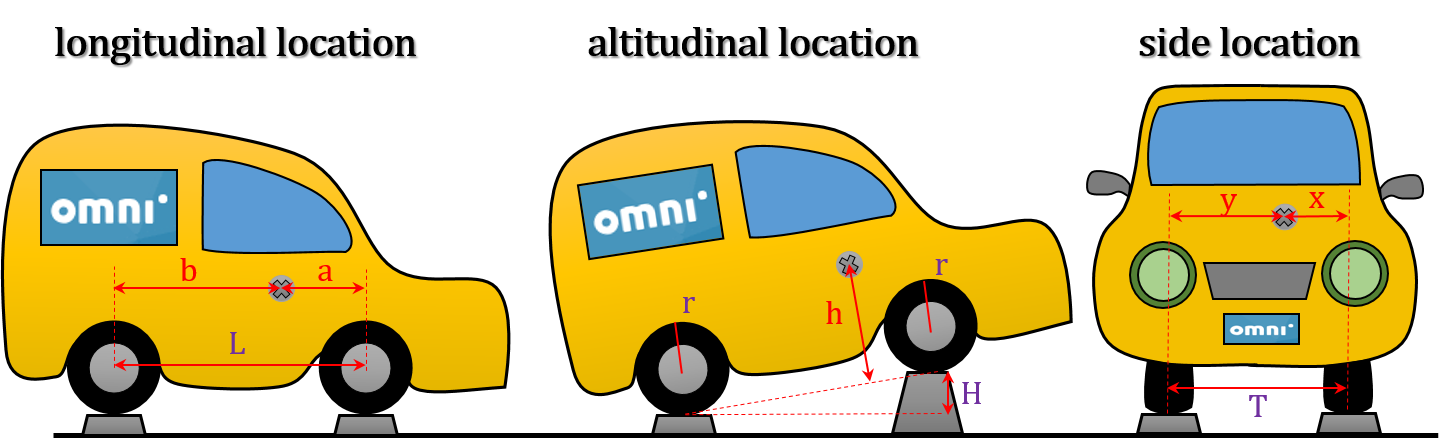
Let's see how to use this car center of mass calculator with an example! This tool can determine the longitudinal, altitudinal and side location of the mass center.

To find the longitudinal location:

1. Begin by entering the car's mass in the Car weight field. For our example, we'll use a mass of 1200 kg.
2. We'll now define the longitudinal position of the car's center of mass. For this, begin by indicating the wheelbase distance. Assume 2.5 m.
3. Enter the Front axle weight. This value should be approximately two times smaller than the total mass of a car. In our case, we'll use 700 kg. The calculator will determine the Rear axle weight. Similarly, if you enter the Rear axle weight, the calculator will find the front one.
4. Now, you'll have the results for the longitudinal position. This one is given by the Distance a (behind the front axle) and Distance b (in front of the rear axle) values. In our example, the car center of mass calculator gives these values: a = 1.0417 m and b = 1.4583 m.

To find the altitudinal location:

1. To find the altitudinal location, first, obtain the longitudinal location by following the steps from the previous section.
2. Choose either Front wheels raised or Rear wheels raised. We're selecting the Front wheels raised for our example.
3. Measure the height of the raised wheels, either the front or rear ones, and enter its value in the Height raised row. In our case, this value is 35 cm.
4. Enter the Wheels radius. For the example, let's assume a radius of 32 cm.
5. Next, input the Front axle weight (wheels raised) or the Rear axle weight (wheels raised). In our case, we're entering a rear weight of 580 kg. The calculator will estimate the weight of the other axle.
6. Once you've entered these values, the calculator will display the Height of the center mass. For our example, this height is 149.88 cm.

To find the side location:

1. Enter the car's mass in the Car weight field. Since we're using the same car as in the previous sections, we input 1200 kg.
2. Proceed to indicate the Car track. This is the distance between the wheels of the same axle. We'll use 1.3 m.
3. Input the Left wheels weight (or Right wheels weight). To weigh your car, drive up onto the scale with either the left or right wheels and measure their weight. Keep in mind that all four wheels should be on the same level. For our example, this value is 700 kg.
4. The resulting distances x and y determine the side position of the center of mass. The results for our example is: x = 0.5417 m and y = 0.7583 m.

The center of mass of an object is an imaginary point at which it's considered that all the object's mass is concentrated. What is the purpose of this concept? Center of mass, like many other concepts in physics and engineering, is a simplification that allows us to make calculations a lot easier. For example, to determine the equilibrium forces applied on an object, we consider these are applied at the center of mass.

Regarding vehicles, the center of mass represents the point where the car's mass is assumed to be concentrated. Knowing the weight distribution is essential as it helps determine the vehicle's stability, performance, braking efficiency, and safety.

Have you ever noticed how race vehicles, particularly Formula One cars, are short and close to the ground? This is because the lower the center of mass, the more stable the car is, and hence the less likely it is to turn over in contrast to vehicles like SUVs and sedans, where the center of mass is positioned higher up.

Now that we've seen what the center of mass is, you might be wondering how to calculate it. One way to find it is with the weighted arithmetic mean. Then, for example, if we want to determine the $x$ coordinate, we can use the following as the center of mass formula:

where:

• $m_i$ – Mass of each of the object's elements; and
• $x_i$ – $x$ position of the center of mass of each mass element measured from a common reference point.

Because we usually specify the center of mass as coordinates, e.g., ($x$, $y$, $z$), we can obtain the $y$ and $z$ values of the center of mass by doing a similar calculation.

We can get the linear momentum by taking the first derivative of the center of mass! Read more about this topic at the impulse and momentum calculator.

Most of the time, the center of mass and center of gravity are in the same location. Keep in mind, however, that this is only true if the gravitational field is uniform (constant). Formally, despite being similar, these two concepts are different. We define the center of gravity as the place at which an object's total weight is concentrated. We can also calculate it using the weighted arithmetic mean as follows:

Here $g_i$ is the gravitational acceleration associated with each element. Note that if the gravitational field is uniform, then the gravitational acceleration is constant, and the same expression will give the center of mass and center of gravity:

Another related concept is the centroid or geometric center of an object. This one and the center of mass will be located in the same position as long as the object's density is uniform. For a non-homogeneous matter distribution, the centroid, the center of mass, and the center of gravity will not match. To find the centroid of an object, we can use this expression:

Where $V_i$ represents the mass of each element that makes up the object, since we can express an object's volume in terms of its density $\rho$ as $V = m/\rho$, if the density is uniform across the volume, then the centroid formula and center of mass formula are the same.