Launch Distance Calculator (Projectile Range)

With this calculator, you can calculate the launch distance (projectile range) without dealing with the complicated physics range equation. Input the velocity, angle of launch, and initial height, and the tool will calculate the launch distance immediately.

Keep reading this article to learn more about:

• What is the range of a projectile; and
• The projectile range formula in physics and its derivation.

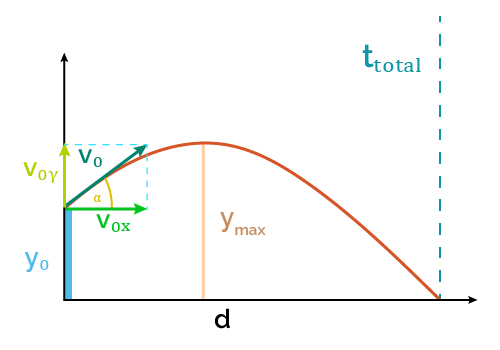
The projectile range is the distance a projectile travels from its launching until it hits the ground. It depends on the launch angle, the initial velocity, the initial height, and the gravitational acceleration.

If you look at the velocity calculator, you'll figure out that distance equals velocity multiplied by time. For a projectile, it's not different: to calculate the launch distance or range ($d$), we multiply the horizontal velocity ($V_{0x}$) by the time of flight ($t_\text{total}$) of the projectile:

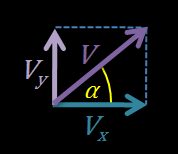
Velocity is a vector we can decompose into its horizontal and vertical components. As they all form a right triangle, the horizontal ($V_{0x}$) and vertical ($V_{0y}$) velocities are related to the initial total velocity ($V_{0}$) and angle of launch ($\alpha$) by the following equations:

And from our time of flight calculator, we know that this variable equals:

where $y_0$ is the initial height of the projectile and $g$ the gravity acceleration ($\approx 9.81 \mathrm{\ m/s^2}$

So, we can combine all the previous equations and obtain a physics formula for the range in terms of the initial velocity, angle of launch, and initial height:

Finally, from the previous section, we obtained our projectile range formula:

, where:

• $d$ — Projectile range or launch distance, calculated in meters ($\text m$) or feet ($\text {ft}$);
• $V_0$ — Initial velocity of the projectile, in meters or feet per second ($\text {m/s}$ or $\text {ft/s}$);
• $\alpha$ — Angle of launch, in radians ($\text {rad}$);
• $y_0$ — Initial height, in $\text m$ or $\text {ft}$; and
• $g$ — Gravity acceleration ($\approx 9.81 \mathrm{\ m/s^2} = 32.2 \mathrm{\ ft/s^2}$).

To convert the angle from degrees to radians, use the following formula $\text{degrees} = \text{radians} \times 180\degree / \pi$, or our angle conversion tool.

Remember that the previous equation doesn't consider the drag forces caused by air resistance. You can learn more about that effect in our free fall with air resistance calculator (for the vertical motion) and the drag equation calculator (for the horizontal displacement).