SUVAT Calculator

Created by Krishna Nelaturu

Last updated: Aug 31, 2022

Table of contents:

What does SUVAT stand for?
SUVAT formulae for velocities
SUVAT formula for displacement
SUVAT formulae without time
SUVAT problems for practice
How to use this SUVAT calculator

Our SUVAT calculator can help you calculate the kinematic equations of motion when the body is accelerating uniformly. This article contains everything you need to know about SUVAT formulae, so grab some snacks and join us below for a brief discussion about:

What does SUVAT stand for?
Deriving SUVAT equations
SUVAT problems

What does SUVAT stand for?

Kinematics is the study of motion without looking at the forces that cause this motion. In this field, the SUVAT equations calculate the linear motion of bodies under constant acceleration. They describe the relationship between the body's

displacement $s$ ,
initial velocity $u$ ,
final velocity $v$ ,
uniform acceleration $a$ , and
time $t$ .

Now can you guess what SUVAT stands for?

There are five SUVAT equations, and we shall derive them individually.

SUVAT formulae for velocities

To describe the initial and final velocities of a body under constant acceleration, consider the following velocity-time graph:

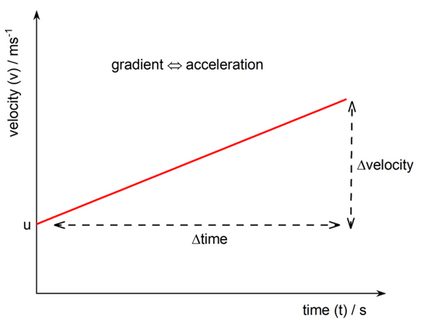
Velocity-time graph of body under constant acceleration. — Figure 1: The velocity time graph of a body under uniform linear acceleration.

The gradient of this graph is equal to the acceleration $a$ . Mathematically:

\begin{align*} a &= \frac{\Delta v}{\Delta t}= \frac{v-u}{\Delta t} \end{align*}

If the motion starts at $t = 0$ and ends at time $t = t$ , we can write:

\begin{align*} a &= \frac{v-u}{t-0} = \frac{v-u}{t} \end{align*}

Rearranging this, we get the first SUVAT equation:

v = u + at

SUVAT formula for displacement

The area under the velocity-time graph in Figure 1 is the displacement of the body. Notice that this area is a trapezoid. The formula for the area of a trapezoid is:

\text{Area} = \text{height} \cdot\frac{(\text{base}_1 + \text{base}_2)}{2}

Looking at the graph from the right side, the base lengths (parallel sides) are $u$ and $v$ , and the height is equal to $t$ . Thus we arrive at the second SUVAT equation:

s = \frac{(u + v)}{2} \cdot t

Substituting the first SUVAT equation here:

\begin{align*} s &= \frac{(u + u + at)}{2} \cdot t\\ &= \frac{2ut + at^2}{2}\\ s &= ut + \frac{1}{2} at^2 \end{align*}

This is the third SUVAT equation. Notice that we can also substitute the relation for initial velocity instead and get the fourth SUVAT equation:

\begin{align*} s &= \frac{(u + v)}{2} \cdot t\\ s &= \frac{(v - at + v)}{2} \cdot t\\ &= \frac{2vt - at^2}{2}\\ s &= vt - \frac{1}{2} at^2 \end{align*}

SUVAT formulae without time

All three SUVAT equations so far involve the variable time $t$ . But what if we don't know the time? So we derive the following SUVAT equation by eliminating $t$ .

Rearranging the first SUVAT equation gives:

t = \frac{v - u}{a}

Substituting this into the trapezoid area formula:

\begin{align*} s &= \frac{(u + v)}{2} \cdot t\\ &= \frac{u + v}{2} \cdot \frac{v - u}{a}\\ s &= \frac{v^2 - u^2}{2a}\\[1em] v^2 &= u^2 + 2as \end{align*}

Let's summarise all five SUVAT equations here:

All SUVAT equations.
S.no	SUVAT equation
1	$v = u + at$
2	$s = \frac{(u + v)}{2} \cdot t$
3	$s = ut + \frac{1}{2}at^2$
4	$s = vt - \frac{1}{2} at^2$
5	$v^2 = u^2 + 2as$

SUVAT problems for practice

Let's go through a couple of SUVAT problems for practice.

A stone dropped from 50 m high freely falls to the ground under gravitational acceleration. With what velocity does it reach the ground, and how long does it take?

What we know:

Height (or displacement) $s = 50 \text{ m}$ .
Initial velocity $u = 0$ .
Acceleration $a = g = 9.81 \text{ m/s}^2$ , if we define positive direction is downwards.

To find:

Final velocity $v$ .
Time $t$ .

Using the fifth SUVAT equation:

\qquad \begin{align*} v^2 &= u^2 + 2as\\ &= 0 + 2 \cdot 9.81 \cdot 50\\ v^2&= 981\\ v &= 31.32 \text{ m/s} \end{align*}

Substituting this in the first SUVAT equation:

\qquad \begin{align*} v &= u + at\\ t & = \frac{v-u}{a} = \frac{31.32-0}{9.81}\\[1em] t &= 3.19 \text{ s} \end{align*}

A squirrel is running away from an unleashed dog. Within 5 seconds, it safely climbs up a tree 20 m away. Both the squirrel and the dog started from rest, and the dog is initially 5 m away from the squirrel. If the squirrel barely made it in time, find out the acceleration of these two animals.

What we know about the squirrel:

Displacement $s_s = 20 \text{ m}$ .
Initial velocity $u_s = 0$ .
Time $t_s = 5 \text{ s}$ .

What we know about the dog:

Displacement $s_d = 25 \text{ m}$ .
Initial velocity $u_d = 0$ .
Time $t_d = 5 \text{ s}$ .

To find:

Acceleration of the two animals.

Rearranging the third SUVAT equation to find acceleration:

\qquad \begin{align*} s &= ut + \frac{1}{2} at^2\\ a &= \frac{2(s - ut)}{t^2} \end{align*}

For the squirrel:

\qquad \begin{align*} a_s &= \frac{2(20 - 0)}{5^2} = \frac{40}{25}\\[1em] a_s &= 1.6 \text{ m/s}^2 \end{align*}

For the dog:

\qquad \begin{align*} a_d &= \frac{2(25 - 0)}{5^2} = \frac{50}{25}\\[1em] a_d &= 2 \text{ m/s}^2 \end{align*}

How to use this SUVAT calculator

This SUVAT calculator is a powerful tool that can calculate all SUVAT equations.

Enter any three known parameters among displacement, initial and final velocities, acceleration, and time, and the calculator will determine the remaining two.
You cannot modify the two calculated values without resetting the whole calculator. Click on the reset button at the bottom left of the calculator.

Interested in more kinematics? Try our projectile motion calculator!

Krishna Nelaturu

If the calculator does not fire after inputting three values, or returns Infinity anywhere, your scenario does not exist in the real world.

Displacement (s)

Initial Velocity (u)

Final Velocity (v)

Acceleration (a)

Time (t)