Gear Ratio Speed Calculator

Our gear ratio speed calculator can help you determine the gear ratio's effect on the speed of the driving or driven shaft. Scroll through the article below to learn more about gear ratio and speed, including:

• What is gear ratio?
• How does gear ratio affect speed?
• Formula for calculating speed from gear ratio.

After reading this article, we're confident you'll design efficient gear systems that are right for your scenarios.

Gears are circular devices with teeth that mesh with each other. They're used to transmit torque or rotational speed. Torque or speed multiplication is an essential aspect of a gear system design. For example, consider the two-gear mechanism below.

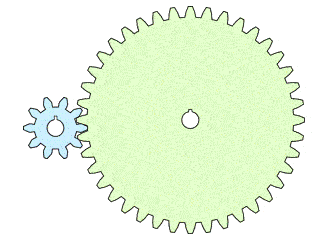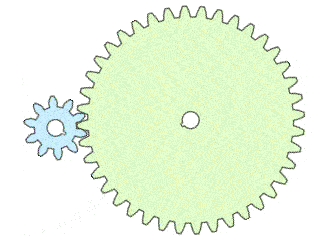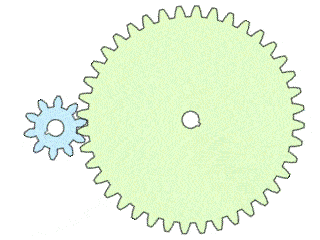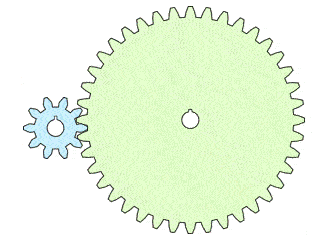
The small gear rotates faster than the large one. If the small gear is the input gear (or driving gear) and the larger gear is the output gear (or driven gear), then speed is reduced in this system. The circumference of the gears plays the determining role here.

Simply put, the gear ratio is the ratio of the circumference of the driving gear (or input gear) to the circumference of the driven gear (or output gear).

Where:

• $D_i$ - Diameter of the input gear; and
• $D_o$ - Diameter of the outer gear.

Since we're interested in the number of teeth on the gear for its design, we can also define gear ratio as the ratio of the number of teeth on the driving gear (or input gear) to the number of teeth on the driven gear (or output gear).

Where:

• $N_i$ - Number of teeth on the input gear; and
• $N_o$ - Number of teeth on the outer gear.

In the following sections, we shall limit our discussion to speed multiplication and gear ratio. You can learn about torque multiplication in a gear system with our gear ratio calculator.

We've seen that a gear's speed is inversely proportional to its size.

where $\omega$ is the gear's angular velocity. Based on this, we can define a velocity ratio:

Where:

• $\omega_i$ - Angular velocity of the input gear; and
• $\omega_o$ - Angular velocity of the output gear.

We can use this gear ratio speed formula to calculate the speed of one gear if we know the speed of the other.

Let's understand how to use gear ratio to calculate speed in RPM with an example:

If there are 27 teeth on the input gear and 12 teeth on the output gear, determine the speed required at the input to maintain a 250 rpm at the output.

Given:

• Number of teeth on the input gear $N_i = 27$.
• Number of teeth on the output gear $N_o = 12$.
• Output speed required $\text{Output rpm} = 250 \text{ rpm}$.

To determine:

• Gear ratio
• Input speed needed.

Let's first find the gear ratio:

Using the relationship between the gear ratio and velocity ratio, let's calculate the input speed:

And that's how you calculate speed from gear ratio!

Using this gear ratio speed calculator is easy. To calculate the gear speed from the gear ratio:

• Enter the number of teeth on the input and output gears.
• Alternatively, you can manually input the gear ratio if it is known.
• Provide the speed of any of the gears to determine the speed of the other.

There are more than one ways to use this calculator. For example, you can determine the gear ratio from the gear speeds! Using this information, you can determine the number of teeth! This practice is common while designing gears!