Tension Calculator

This string tension calculator will help you find how much of a tension force a string or rope experiences when subjected to pulling or stretching forces. In this calculator, you will learn:

• What tension is;
• How to calculate tension force;
• What the tension force formula is; and
• How to use this string tension calculator.

Keep on reading to start learning.

Tension is an axial force brought by the action of pulling an object apart. We can observe this on ropes, strings, or structural components like trusses, beams, and bolts. As long as an object is subject to pulling force, that object is also subject to a tension force.

A string attached to the ceiling to hang an object experiences tension force due to the pull of gravity onto the hanging object. Without the string, the object will just free fall to the ground. Attaching the object to two strings will distribute the tension force to the two strings at proportions depending on the angles the strings have from the ceiling line. Your arm can also experience tension when lifting objects from the ground or dragging them across the ground.

Find out how to find tension in a rope or any similar material in the next section of this text.

To calculate tension forces is basically utilizing Newton's Second Law of Motion, where the force an object experiences (or can deliver) equates to the product of the mass and acceleration of that object.

We can observe tension forces in lots of situations. To understand the concept better, we'll focus on cases where we hang an object from a supporting surface and when we drag things across a surface.

Hanging an object

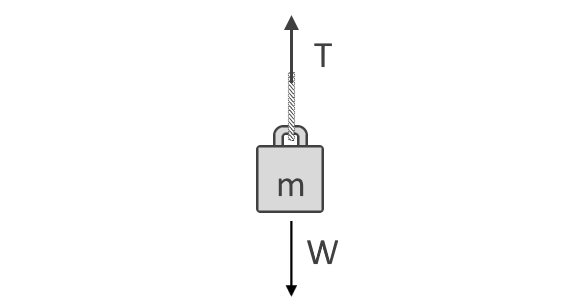
Imagine an object hanging from the ceiling. The object's weight, which we can denote as $W$, is equal to its mass, $m$, multiplied by the gravitational acceleration $g$. The tension force, $T$, the rope experiences is equal to that, as shown in this free-body diagram:

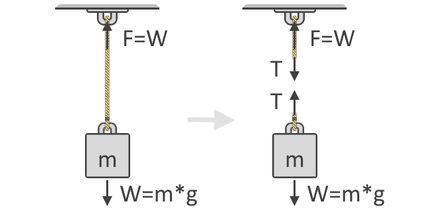
From that illustration, we can say that the formula for string tension force from a hanging object is:

But what if the object hangs on more than one rope? For that, the sum of all the tension forces across the ropes should equal the object's weight. To illustrate that, let's look at the free-body diagram of this object attached to two ropes:

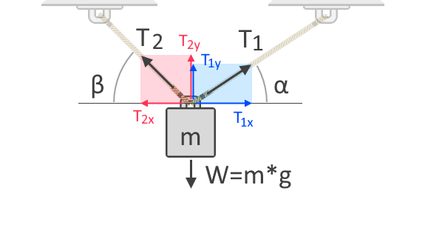
Since tension is an axial force, the sum of all the forces along the direction of this force, in this case, along the vertical axis, should be in equilibrium. That means that the forces in a vertically downward direction should be equal to the upward direction forces. In equation form, we express that as:

where:

• $W$ is the weight of the object;
• $m$ is the mass of the object;
• $g$ is the gravitational acceleration;
• $T_{1y}$ is the vertical component of the tension force $T_1$;
• $T_{2y}$ is the vertical component of tension force $T_2$;
• $\alpha$ is $T_1$'s angle of inclination; and
• $\beta$ is $T_2$'s angle of inclination.

We also need to note that along the horizontal, the object must be in equilibrium too. That means:

With these relationships between $T_1$ and $T_2$ in mind, we can derive two formulas we can use to find each of their values given the other parameters mentioned previously. Here are those two tension force formulas:

Pulling an object

Pulling an object across a surface is very similar to hanging an object. However, instead of the object's weight as the primary source of the force that contributes to the tension force, this time, we consider an applied pulling force. And like before, we also consider our system to be in equilibrium, such that when we consider a free-body diagram, its summation of forces should be equal to zero. For this case, we assume our ropes don't have mass, and the surface we drag our objects on has no friction.

The first step in calculating the rope or string tension force when pulling an object is to find the acceleration, $a$ of the object. We can do that by dividing our pulling force, $T$, by the mass of the object, $m$:

If we're pulling a single object, the tension force the rope will experience will basically be equal to the pulling force, even if the direction of force is at a slope. Adding another object by attaching it to our first one using another rope will increase the tension force on the first rope, and we'll need more pulling force to drag both objects. Also, there will be a different tension force on the rope between the two objects, as we can see in an example illustration below:

For such a situation, we first calculate the acceleration of the system by dividing the horizontal component of the 24-newton pulling force, $T_\text{x}$, by the total mass of the system, which is equal to 5 kilograms:

As mentioned earlier, the tension force within the first rope, $T_1$, is equal to the pulling force of $24\ \text{N}$.

On the other hand, we can calculate the tension force within the second rope, $T_2$, by utilizing Newton's Second Law of Motion again. In that case, we get $T_2 = 2\ \text{kg}\times 2.4\ \frac{\text{m}}{\text{s}^2} = 4.8\ \text{N}$

You can use our string tension calculator for both situations we discussed earlier. Select Object is hanging or Pulling on a frictionless surface depending on what you are interested in calculating. Here are the next steps on how to find tension in a rope using our calculator:

For the object is hanging option:

1. Select the number of ropes that holds your object.
2. Enter the mass of your object.
3. If you selected 2 ropes in step number 1, you'd have to input the values for the angles $\alpha$ and $\beta$.
4. If you want to be specific on the gravitational acceleration you want to use in the calculation, you can modify our default value of 9.806 m/s² by clicking on the Advanced mode button below our tool.

For pulling on a frictionless surface option:

1. Choose the number of objects pulled in the system.
2. Enter the masses of your objects.
3. Input the pulling force applied to the system.
4. Type in the angle of inclination of the pulling force.