Compressibility Factor Calculator

Welcome to the compressibility factor calculator, a tool created to calculate the compressibility factor of gases, also known as compression factor, gas deviation factor, or simply Z-factor.

Calculating the Z-factor is the most straightforward way to quantify the deviation of a gas from the ideal gas law behavior. In the following sections of this article, we talk about this deviation, the equation for the compressibility factor, and the air compressibility factor values.

The widely-known ideal gas law is an idealization of the complex behavior of gases. Depending on the temperature, pressure, and type of substance, gases will behave more or less according to that idealization. The compressibility factor is the tool that quantifies that deviation from the ideal behavior.

Depending on the field of study, the form of the compressibility factor equation used will vary. For example, in statistical mechanics (and this calculator), the compressibility factor formula is:

, where:

• $p$ — Pressure, in pascals (Pa);
• $V$ — Volume, in cubic meters (m³);
• $n$ — Number of moles of gas, in mol;
• $\bar R$ — Universal gas constant, whose value equals 8.3144626 J/(mol K);
• $T$ - Absolute temperature of the gas, in kelvin (K); and
• $Z$ — Compressibility factor (calculated as dimensionless quantity).

In engineering thermodynamics, the commonly used formula for the compressibility factor is:

where:

• $\rho$ — Gas density, in kilograms per cubic meter (m³); and
• $R_{\text{specific}}$ — Specific gas constant of the gas, in J/(kg K);

If Z = 1, by definition, the gas behaves perfectly as an ideal gas. The farther Z is from unity, the less it will act as an ideal gas. Values far from Z = 1 correspond to pressures and temperatures near the critical point. You can figure this out in the compressibility chart in the following section.

With this compressibility factor calculator, we can calculate the Z-factor if we conduct measurements of the pressure, volume, mass (for the number of moles), and temperature.

If we only know the temperature and pressure, we can still calculate it using a compressibility chart.

A compressibility chart contains values for Z as a function of the reduced pressure (pᵣ) and reduced temperature (Tᵣ), defined as:

• pᵣ = p/p_c
• Tᵣ = T/T_c

where p_c is the critical pressure and T_c is the critical temperature. p_c and T_c are the pressure and temperature values of the critical point of the substance.

Thanks to the theorem of corresponding states, we can use the previous chart for any gas, but if we're only studying the compressibility of air, we can use a chart that doesn't require knowing p_c and T_c.

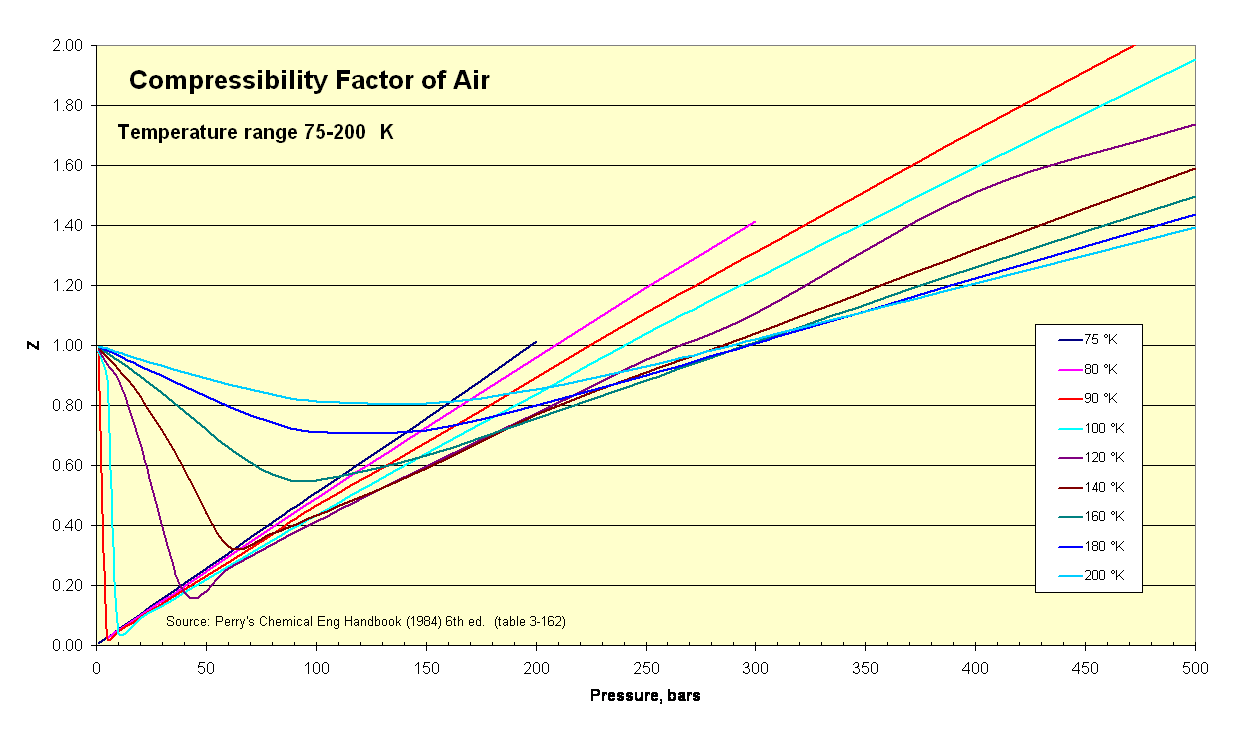
Using those charts, we can obtain the compressibility of gases by only knowing the temperature and pressure.