Heisenberg's Uncertainty Principle Calculator

With Heisenberg's uncertainty principle calculator, you will learn about one of the most fundamental quantum mechanics concepts. We say "fundamental" not to write "controversial" and "mind-blowing". Follow us in this short article to learn:

• What is Heisenberg's uncertainty principle: formula and definition;
• How do we calculate Heisenberg's uncertainty principle;
• Why does the observer don't matter in the definition of Heisenberg's uncertainty principle; and
• How to use Heisenberg's uncertainty principle: examples of real-world situations.

The quantum nature of objects is (most of the time) hidden from our eyes. We have to zoom in to discover it and its effect. Past the structure of our material, past the molecular scale, and finally, at an atomic scale. Here, the laws of classical physics are merely a suggestion: you can cross walls, pop into existence from a vacuum, and so on.

One of the fundamental reasons for the quantum world to be so distant from our usual understanding is that everything has a double nature on a quantum scale: subatomic particles behave both as particles and as waves. This peculiarity is progressively less relevant for objects of increasing size, nevertheless still existing. We can define a wavelength for every object: our De Broglie wavelength calculator explains how!

Heisenberg's uncertainty principle is a fundamental consequence of the probabilistic nature of quantum objects. We hook on the De Broglie equation to explain it. The equation that assigns a wavelength to every object with particle-wave dualism is:

where:

• $p$ — The momentum measured in $\mathrm{kg\cdot m/s}$;
• $h$ — The Planck's constant, a physical constant at the base of quantum phenomena ($h = 6.62607015×10−34\ \mathrm{J/Hz}$); and
• $\lambda$ — The De Broglie wavelength.

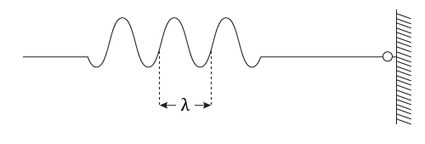
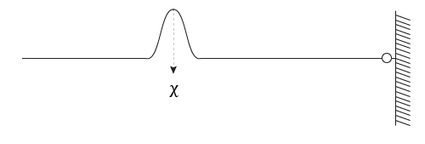
This relation connects the momentum and the wavelength of the object in analysis. Now think of a practical example. Tie a rope to a wall, pull on the other end, and shake it. First, do it slowly: you will create a nice wave. This wave has a very well-defined wavelength (or momentum, if you look at it through the De Broglie equation) but an ill-defined position. Where is the wave? On the rope, but where? Now give it a jerk: the small dent is not even a wave as we understand it, and defining its wavelength (momentum!) is not easy. On the other side, apart from a small spread, its position is easily measurable.

Now, imagine an object that can be both things at the same time: that's a quantum particle. The lack of precision on the momentum lives along with the lack of precision on the position along the rope.

The mathematics behind Heisenberg's uncertainty principle formula is not the easiest one. We will first give you the equation: the explanation comes later! You will see Heisenberg's uncertainty principle equation in two forms in your physics studies. Let's see the first one:

where $Δx$ and $Δp$ are uncertainties. The modern formulation (and what we regularly use to calculate Heisenberg's uncertainty principle) uses the reduced Planck's constant $\hbar = h/2\pi$ and substitutes the uncertainties of the variables with their standard deviations:

When calculating Heisenberg's uncertainty principle, we use this inequality's lowest bound. The equality between the two sides represents the highest possible quality of information on the two variables: the nature of our particle would prevent us from arbitrarily reducing the uncertainty of the variables: once their product reaches that bound, one of the two begins rising.

Intuitively, you can think of the behavior of the particle as follows:

• If undisturbed, your quantum particle would look like a blurry dot moving in an unspecified direction;
• If you try to fix its velocity, you will find out that the blurred spot increased in size: the uncertainty in position got worse!
• Try to pinpoint the particle in space. Now its position is well-defined, but the particle is trying to escape in all directions at the same time! The momentum is not defined as well as before.
• What if you try to decrease both at the same tim... you can't!

To use our Heisenberg's uncertainty principle calculator, you have to know the values of the uncertainty of one of three possible quantities:

• The momentum;
• The position; or
• The velocity.

If you are using the velocity, you will also have to define the mass of the object: we will use these two quantities to calculate the momentum uncertainty

Once you input the variables necessary to compute the equality, we will output the result of the lowest possible uncertainty on the other variable(s):

A short note: $\hbar$, being a constant of the quantum world, has a very small value: $\hbar =1.05457182 \times10^{-34}\ \mathrm{m^2 kg / s}$. Be careful when inserting large values of uncertainties (large from a microscopic point of view): the other quantities will easily go to $0$ as a consequence. This calculator is best suited to operate for particles and atoms than for cars and squirrels!

The definition of Heisenberg's uncertainty principle equation was, for a long time, associated with the presence of an observer. Usually, we are taught that if an observer zeroes in the position, the momentum of the particle skyrockets, and vice-versa. Well, that's not precisely true. It's not the observer that causes this phenomenon: the way we define Heisenberg's uncertainty principle rules out the observer altogether. The origin of the uncertainty relation stems from the probabilistic wave-like nature of quantum objects.

What depends on the measurement is the observer effect, which causes a quantum wavefunction to collapse in a single state.

Take an electron traveling at $20$ the speed of light with an uncertainty of $Δv = 0.12$ of $c$. We know the mass of an electron $m_\mathrm{e}= 9.109\times10^{-31}\ \mathrm{kg}$. The uncertainty on the momentum then becomes:

Let's apply Heisenberg's uncertainty principle formula to find the uncertainty on the position of our electron. As said in the previous sections, we will use the limit case of the equality:

Invert this equation and substitute the values we found before:

This value is around one hundred thousand times bigger than the electron radius used in most calculations (notice that the electron, most likely, has no size at all: we assign one when we need to consider its interactions).